Topology User Manual¶
The Topology Module provides the NEST simulator 1 with a convenient interface for creating layers of neurons placed in space and connecting neurons in such layers with probabilities and properties depending on the relative placement of neurons. This permits the creation of complex networks with spatial structure.
This user manual provides an introduction to the functionality provided by the Topology Module. It is based exclusively on the PyNEST, the Python interface to NEST. NEST users using the SLI interface should be able to map instructions to corresponding SLI code. This manual is not meant as a comprehensive reference manual. Please consult the online documentation in PyNEST for details; where appropriate, that documentation also points to relevant SLI documentation.
This manual describes the Topology Module included with NEST 2.16; the user interface and behavior of the module has not changed significantly since NEST 2.2.
In the next chapter of this manual, we introduce Topology layers, which place neurons in space. In Chapter 3 we then describe how to connect layers with each other, before discussing in Chapter 4 how you can inspect and visualize Topology networks. Chapter 5 deals with the more advanced topic of extending the Topology module with custom kernel functions and masks provided by C++ classes in an extension module.
You will find the Python scripts used in the examples in this manual in
the NEST source code directory under
doc/topology/user_manual_scripts.
Limitations and Disclaimer¶
- Undocumented features
The Topology Module provides a number of undocumented features, which you may discover by browsing the code. These features are highly experimental and should not be used for simulations, as they have not been validated.
Layers¶
The Topology Module (just Topology for short in the remainder of this document) organizes neuronal networks in layers. We will first illustrate how Topology places elements in simple layers, where each element is a single model neuron. Layers with composite elements are discussed in the following section.
We will illustrate the definition and use of layers using examples.
Topology distinguishes between two classes of layers:
- grid-based layers
in which each element is placed at a location in a regular grid;
- free layers
in which elements can be placed arbitrarily in the plane.
Grid-based layers allow for more efficient connection-generation under certain circumstances.
Grid-based Layers¶
We create a first, grid-based simple layer with the following commands:
import nest.topology as tp
l = tp.CreateLayer({'rows': 5,
'columns': 5,
'elements': 'iaf_psc_alpha'})
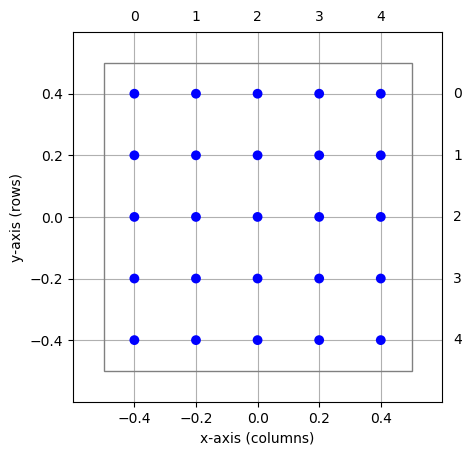
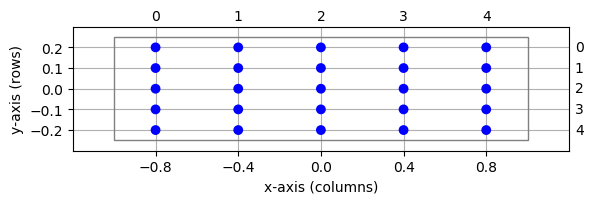
Figure 10 Simple grid-based layer centered about the origin. Blue circles mark layer elements, the thin square the extent of the layer. Row and column indices are shown in the right and top margins, respectively.¶
The layer is shown in Figure 10. Note the following properties:
The layer has five rows and five columns.
The
'elements'entry of the dictionary passed toCreateLayerdetermines the elements of the layer. In this case, the layer containsiaf_psc_alphaneurons.The center of the layer is at the origin of the coordinate system, \((0,0)\).
The extent or size of the layer is \(1\times 1\). This is the default size for layers. The extent is marked by the thin square in Figure 10.
The grid spacing of the layer is
In the layer shown, we have \(dx=dy=0.2\), but the grid spacing may differ in x- and y-direction.
Layer elements are spaced by the grid spacing and are arranged symmetrically about the center.
The outermost layer elements are placed \(dx/2\) and \(dy/2\) from the borders of the extent.
Element positions in the coordinate system are given by \((x,y)\) pairs. The coordinate system follows that standard mathematical convention that the \(x\)-axis runs from left to right and the \(y\)-axis from bottom to top.
Each element of a grid-based layer has a row- and column-index in addition to its \((x,y)\)-coordinates. Indices are shown in the top and right margin of Figure 10. Note that row-indices follow matrix convention, i.e., run from top to bottom. Following pythonic conventions, indices run from 0.
Layers have a default extent of \(1\times 1\). You can specify a
different extent of a layer, i.e., its size in \(x\)- and
\(y\)-direction by adding an 'extent' entry to the dictionary
passed to CreateLayer:
l = tp.CreateLayer({'rows': 5,
'columns': 5,
'extent': [2.0, 0.5],
'elements': 'iaf_psc_alpha'})
The resulting layer is shown in Figure 11. The extent is always a two-element tuple of floats. In this example, we have grid spacings \(dx=0.4\) and \(dy=0.1\). Changing the extent does not affect grid indices.
The size of 'extent' in \(x\)- and \(y\)-directions should
be numbers that can be expressed exactly as binary fractions. This is
automatically ensured for integer values. Otherwise, under rare
circumstances, subtle rounding errors may occur and trigger an
assertion, thus stopping NEST.
Layers are centered about the origin \((0,0)\) by default. This can
be changed through the 'center' entry in the dictionary specifying
the layer. The following code creates layers centered about
\((0,0)\), \((-1,1)\), and \((1.5,0.5)\), respectively:
l1 = tp.CreateLayer({'rows': 5,
'columns': 5,
'elements': 'iaf_psc_alpha'})
l2 = tp.CreateLayer({'rows': 5,
'columns': 5,
'elements': 'iaf_psc_alpha',
'center': [-1., 1.]})
l3 = tp.CreateLayer({'rows': 5,
'columns': 5,
'elements': 'iaf_psc_alpha',
'center': [1.5, 0.5]})
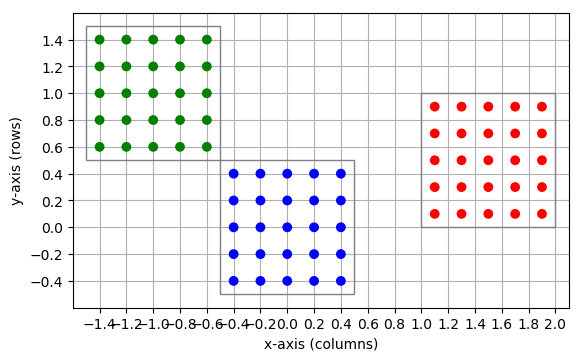
Figure 12 Three layers centered, respectively, about \((0,0)\) (blue), \((-1,-1)\) (green), and \((1.5,0.5)\) (red).¶
The center is given as a two-element tuple of floats. Changing the center does not affect grid indices: For each of the three layers in Figure 12, grid indices run from 0 to 4 through columns and rows, respectively, even though elements in these three layers have different positions in the global coordinate system.
The 'center' coordinates should be numbers that can be expressed
exactly as binary fractions. For more information, see
Sec. 2.1.2.
To see how to construct a layer, consider the following example:
a layer with \(n_r\) rows and \(n_c\) columns;
spacing between nodes is \(d\) in \(x\)- and \(y\)-directions;
the left edge of the extent shall be at \(x=0\);
the extent shall be centered about \(y=0\).
From Eq. dx_dy_extent, we see that the extent of the layer must be
\((n_c d, n_r d)\). We now need to find the coordinates
\((c_x, c_y)\) of the center of the layer. To place the left edge of
the extent at \(x=0\), we must place the center of the layer at
\(c_x=n_c d / 2\) along the \(x\)-axis, i.e., half the extent
width to the right of \(x=0\). Since the layer is to be centered
about \(y=0\), we have \(c_y=0\). Thus, the center coordinates
are \((n_c d/2, 0)\). The layer is created with the following code
and shown in Figure 13:
nc, nr = 5, 3
d = 0.1
l = tp.CreateLayer({'columns': nc,
'rows': nr,
'elements': 'iaf_psc_alpha',
'extent': [nc * d, nr * d],
'center': [nc * d / 2., 0.]})
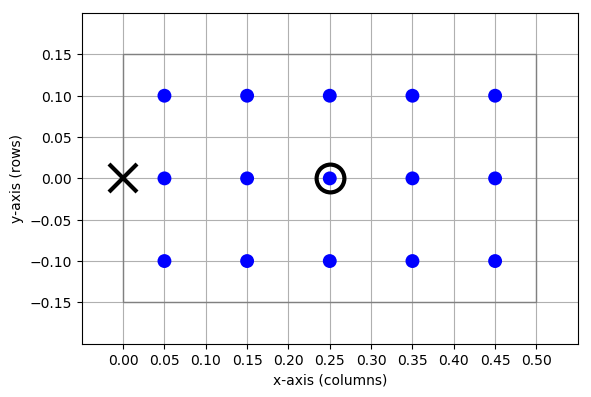
Figure 13 Layer with \(n_c=5\) rows and \(n_r=3\) columns, spacing \(d=0.1\) and the left edge of the extent at \(x=0\), centered about the \(y\)-axis. The cross marks the point on the extent placed at the origin \((0,0)\), the circle the center of the layer.¶
Free layers¶
Free layers do not restrict node positions to a grid, but allow free
placement within the extent. To this end, the user needs to specify the
positions of all nodes explicitly. The following code creates a layer of
50 iaf_psc_alpha neurons uniformly distributed in a layer with
extent \(1\times 1\), i.e., spanning the square
\([-0.5,0.5]\times[-0.5,0.5]\):
import numpy as np
pos = [[np.random.uniform(-0.5, 0.5), np.random.uniform(-0.5, 0.5)]
for j in range(50)]
l = tp.CreateLayer({'positions': pos,
'elements': 'iaf_psc_alpha'})
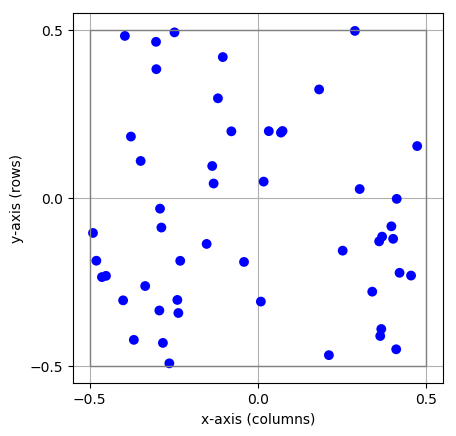
Figure 14 A free layer with 50 elements uniformly distributed in an extent of size \(1\times 1\).¶
Note the following points:
For free layers, element positions are specified by the
'positions'entry in the dictionary passed toCreateLayer.'positions'is mutually exclusive with'rows'/'columns'entries in the dictionary.The
'positions'entry must be a Pythonlist(ortuple) of element coordinates, i.e., of two-element tuples of floats giving the (\(x\), \(y\))-coordinates of the elements. One layer element is created per element in the'positions'entry.All layer element positions must be within the layer’s extent. Elements may be placed on the perimeter of the extent as long as no periodic boundary conditions are used; see Sec. 2.4.
Element positions in free layers are not shifted when specifying the
'center'of the layer. The user must make sure that the positions given lie within the extent when centered about the given center.
3D layers¶
Although the term “layer” suggests a 2-dimensional structure, the layers in NEST may in fact be 3-dimensional. The example from the previous section may be easily extended with another component in the coordinates for the positions:
import numpy as np
pos = [[np.random.uniform(-0.5, 0.5), np.random.uniform(-0.5, 0.5),
np.random.uniform(-0.5, 0.5)] for j in range(200)]
l = tp.CreateLayer({'positions': pos,
'elements': 'iaf_psc_alpha'})
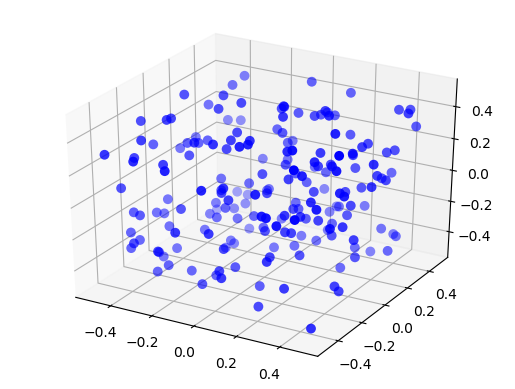
Figure 15 A free 3D layer with 200 elements uniformly distributed in an extent of size \(1\times 1\times 1\).¶
Periodic boundary conditions¶
Simulations usually model systems much smaller than the biological networks we want to study. One problem this entails is that a significant proportion of neurons in a model network is close to the edges of the network with fewer neighbors than nodes properly inside the network. In the \(5\times 5\)-layer in Figure 10, e.g., 16 out of 25 nodes form the border of the layer.
One common approach to reducing the effect of boundaries on simulations is to introduce periodic boundary conditions, so that the rightmost elements on a grid are considered nearest neighbors to the leftmost elements, and the topmost to the bottommost. The flat layer becomes the surface of a torus. Figure 16 illustrates this for a one-dimensional layer, which turns from a line to a ring upon introduction of periodic boundary conditions.
You specify periodic boundary conditions for a layer using the
dictionary entry edge_wrap:
lp = tp.CreateLayer({'rows': 1, 'columns': 5, 'extent': [5., 1.],
'elements': 'iaf_psc_alpha',
'edge_wrap': True})
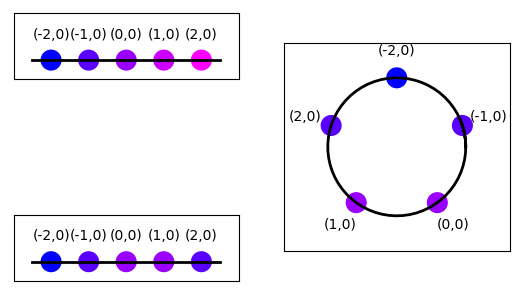
Figure 16 Top left: Layer with single row and five columns without periodic boundary conditions. Numbers above elements show element coordinates. Colors shifting from blue to magenta mark increasing distance from the element at \((-2,0)\). Bottom left: Same layer, but with periodic boundary conditions. Note that the element at \((2,0)\) now is a nearest neighbor to the element at \((-2,0)\). Right: Layer with periodic boundary condition arranged on a circle to illustrate neighborhood relationships.¶
Note that the longest possible distance between two elements in a layer without periodic boundary conditions is
but only
for a layer with periodic boundary conditions; \(x_{\text{ext}}\) and \(y_{\text{ext}}\) are the components of the extent size.
We will discuss the consequences of periodic boundary conditions more in Chapter 3.
From the perspective of NEST, a Topology layer is a special type of subnet. From the user perspective, the following points may be of interest:
Grid-based layers have the NEST model type
topology_layer_grid, free layers the model typetopology_layer_free.The status dictionary of a layer has a
'topology'entry describing the layer properties (lis the layer created above):
print(nest.GetStatus(l)[0]['topology'])
{'center': (0.0, 0.0), 'columns': 5, 'depth': 1, 'edge_wrap': False, 'extent': (1.0, 1.0), 'rows': 5}
The ‘topology’ entry is read-only.
The NEST kernel sees the elements of the layer in the same way as the elements of any subnet. You will notice this when printing a network with a Topology layer:
nest.PrintNetwork(depth=3)
+-[0] root dim=[1 25]
|
+-[1] topology_layer_grid dim=[25]
|
+-[1]...[25] iaf_psc_alpha
The 5 times 5 layer created above appears here as a topology_layer_grid subnet of 25 iaf_psc_alpha neurons. Only Topology connection and visualization functions heed the spatial structure of the layer.
Layers with composite elements¶
So far, we have considered layers in which each element was a single model neuron. Topology can also create layers with composite elements, i.e., layers in which each element is a collection of model neurons, or, in general NEST network nodes.
Construction of layers with composite elements proceeds exactly as for
layers with simple elements, except that the 'elements' entry of the
dictionary passed to CreateLayer is a Python list or tuple. The
following code creates a \(1\times 2\) layer (to keep the output
from PrintNetwork() compact) in which each element consists of one
'iaf_cond_alpha' and one 'poisson_generator' node
l = tp.CreateLayer({'rows': 1, 'columns': 2,
'elements': ['iaf_cond_alpha',
'poisson_generator']})
+-[0] root dim=[1 4]
|
+-[1] topology_layer_grid dim=[4]
|
+-[1]...[2] iaf_cond_alpha
+-[3]...[4] poisson_generator
The network consist of one topology_layer_grid with four elements:
two iaf_cond_alpha and two poisson_generator nodes. The
identical nodes are grouped, so that the subnet contains first one full
layer of iaf_cond_alpha nodes followed by one full layer of
poisson_generator nodes.
You can create network elements with several nodes of each type by following a model name with the number of nodes to be created:
l = tp.CreateLayer({'rows': 1, 'columns': 2,
'elements': ['iaf_cond_alpha', 10,
'poisson_generator',
'noise_generator', 2]})
+-[0] root dim=[1 26]
|
+-[1] topology_layer_grid dim=[26]
|
+-[1]...[20] iaf_cond_alpha
+-[21]...[22] poisson_generator
+-[23]...[26] noise_generator
In this case, each layer element consists of 10 iaf_cond_alpha
neurons, one poisson_generator, and two noise_generators.
Note the following points:
Each element of a layer has identical components.
All nodes within a composite element have identical positions, namely the position of the layer element.
When inspecting a layer as a subnet, the different nodes will appear in groups of identical nodes.
For grid-based layers, the function
GetElementreturns a list of nodes at a given grid position. See Chapter 4 for more on inspecting layers.In a previous version of the topology module it was possible to create layers with nested, composite elements, but such nested networks gobble up a lot of memory for subnet constructs and provide no practical advantages, so this is no longer supported. See the next section for design recommendations for more complex layers.
A paper on a neural network model might describe the network as follows 2:
The network consists of \(20x20\) microcolumns placed on a regular grid spanning \(0.5^\circ\times 0.5^\circ\) of visual space. Neurons within each microcolumn are organized into L2/3, L4, and L56 subpopulations. Each subpopulation consists of three pyramidal cells and one interneuron. All pyramidal cells are modeled as NEST
iaf_psc_alphaneurons with default parameter values, while interneurons areiaf_psc_alphaneurons with threshold voltage \(V_{\text{th}}=-52\)mV.
How should you implement such a network using the Topology module? The recommended approach is to create different models for the neurons in each layer and then define the microcolumn as one composite element:
for lyr in ['L23', 'L4', 'L56']:
nest.CopyModel('iaf_psc_alpha', lyr + 'pyr')
nest.CopyModel('iaf_psc_alpha', lyr + 'in', {'V_th': -52.})
l = tp.CreateLayer({'rows': 20, 'columns': 20, 'extent': [0.5, 0.5],
'elements': ['L23pyr', 3, 'L23in',
'L4pyr', 3, 'L4in',
'L56pyr', 3, 'L56in']})
We will discuss in Chapter 3.1 how to connect selectively to different neuron models.
Connections¶
The most important feature of the Topology module is the ability to
create connections between layers with quite some flexibility. In this
chapter, we will illustrate how to specify and create connections. All
connections are created using the ConnectLayers function.
Basic principles¶
We begin by introducing important terminology:
- Connection
In the context of connections between the elements of Topology layers, we often call the set of all connections between pairs of network nodes created by a single call to
ConnectLayersa connection.- Connection dictionary
A dictionary specifying the properties of a connection between two layers in a call to
CreateLayers.- Source
The source of a single connection is the node sending signals (usually spikes). In a projection, the source layer is the layer from which source nodes are chosen.
- Target
The target of a single connection is the node receiving signals (usually spikes). In a projection, the target layer is the layer from which target nodes are chosen.
- Connection type
The connection type determines how nodes are selected when
ConnectLayerscreates connections between layers. It is either'convergent'or'divergent'.- Convergent connection
When creating a convergent connection between layers, Topology visits each node in the target layer in turn and selects sources for it in the source layer. Masks and kernels are applied to the source layer, and periodic boundary conditions are applied in the source layer, provided that the source layer has periodic boundary conditions.
- Divergent connection
When creating a divergent connection, Topology visits each node in the source layer and selects target nodes from the target layer. Masks, kernels, and boundary conditions are applied in the target layer.
- Driver
When connecting two layers, the driver layer is the one in which each node is considered in turn.
- Pool
- When connecting two layers, the pool layer is the one from which nodes are chosen for each node in the driver layer. I.e., we have
Connection type
Driver
Pool
convergent
target layer
source layer
divergent
source layer
target layer
- Displacement
The displacement between a driver and a pool node is the shortest vector connecting the driver to the pool node, taking boundary conditions into account.
- Distance
The distance between a driver and a pool node is the length of their displacement.
- Mask
The mask defines which pool nodes are at all considered as potential targets for each driver node. See Sec. 3.3 for details.
- Kernel
The kernel is a function returning a (possibly distance- or displacement-dependent) probability for creating a connection between a driver and a pool node. The default kernel is \(1\), i.e., connections are created with certainty. See Sec. 3.4 for details.
- Autapse
An autapse is a synapse (connection) from a node onto itself. Autapses are permitted by default, but can be disabled by adding
'allow_autapses': Falseto the connection dictionary.- Multapse
Node A is connected to node B by a multapse if there are synapses (connections) from A to B. Multapses are permitted by default, but can be disabled by adding
'allow_multapses': Falseto the connection dictionary.
Connections between Topology layers are created by calling
ConnectLayers with the following arguments 3:
The source layer.
The target layer (can be identical to source layer).
A connection dictionary that contains at least the following entry:
- ‘connection_type’
either
'convergent'or'divergent'.
In many cases, the connection dictionary will also contain
- ‘mask’
a mask specification as described in Sec. 3.3.
Only neurons within the mask are considered as potential sources or targets. If no mask is given, all neurons in the respective layer are considered sources or targets.
Here is a simple example, cf. Figure 17
l = tp.CreateLayer({'rows': 11, 'columns': 11, 'extent': [11., 11.],
'elements': 'iaf_psc_alpha'})
conndict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-2., -1.],
'upper_right': [2., 1.]}}}
tp.ConnectLayers(l, l, conndict)
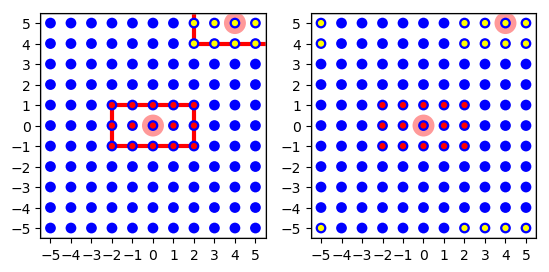
Figure 17 Left: Minimal connection example from a layer onto itself using a rectangular mask shown as red line for the node at \((0,0)\) (marked light red). The targets of this node are marked with red dots. The targets for the node at \((4,5)\) are marked with yellow dots. This node has fewer targets since it is at the corner and many potential targets are beyond the layer. Right: The effect of periodic boundary conditions is seen here. Source and target layer and connection dictionary were identical, except that periodic boundary conditions were used. The node at \((4,5)\) now has 15 targets, too, but they are spread across the corners of the layer. If we wrapped the layer to a torus, they would form a \(5\times 3\) rectangle centered on the node at \((4,5)\).¶
In this example, layer l is both source and target layer. Connection
type is divergent, i.e., for each node in the layer we choose targets
according to the rectangular mask centered about each source node. Since
no connection kernel is specified, we connect to all nodes within the
mask. Note the effect of normal and periodic boundary conditions on the
connections created for different nodes in the layer, as illustrated in
Figure 17.
Mapping source and target layers¶
The application of masks and other functions depending on the distance or even the displacement between nodes in the source and target layers requires a mapping of coordinate systems between source and target layers. Topology applies the following coordinate mapping rules:
All layers have two-dimensional Euclidean coordinate systems.
No scaling or coordinate transformation can be applied between layers.
The displacement \(d(D,P)\) from node \(D\) in the driver layer to node \(P\) in the pool layer is measured by first mapping the position of \(D\) in the driver layer to the identical position in the pool layer and then computing the displacement from that position to \(P\). If the pool layer has periodic boundary conditions, they are taken into account. It does not matter for displacement computations whether the driver layer has periodic boundary conditions.
Masks¶
A mask describes which area of the pool layer shall be searched for nodes to connect for any given node in the driver layer. We will first describe geometrical masks defined for all layer types and then consider grid-based masks for grid-based layers. If no mask is specified, all nodes in the pool layer will be searched.
Note that the mask size should not exceed the size of the layer when using periodic boundary conditions, since the mask would “wrap around” in that case and pool nodes would be considered multiple times as targets.
If none of the mask types provided in the topology library meet your need, you may add more mask types in a NEST extension module. This is covered in Chapter 5.
Topology currently provides four types of masks usable for 2-dimensional free and grid-based layers. They are illustrated in Figure 18. The masks are
- Rectangular
All nodes within a rectangular area are connected. The area is specified by its lower left and upper right corners, measured in the same unit as element coordinates. Example:
conndict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-2., -1.],
'upper_right': [2., 1.]}}}
- Circular
All nodes within a circle are connected. The area is specified by its radius.
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 2.0}}}
- Doughnut
All nodes between an inner and outer circle are connected. Note that nodes on the inner circle are not connected. The area is specified by the radii of the inner and outer circles.
conndict = {'connection_type': 'divergent',
'mask': {'doughnut': {'inner_radius': 1.5,
'outer_radius': 3.}}}
- Elliptical
All nodes within an ellipsis are connected. The area is specified by its major and minor axis. Note that this mask was added to NEST with NEST 2.14.
conndict = {'connection_type': 'divergent',
'mask': {'elliptical': {'major_axis': 7.,
'minor_axis': 4.}}}
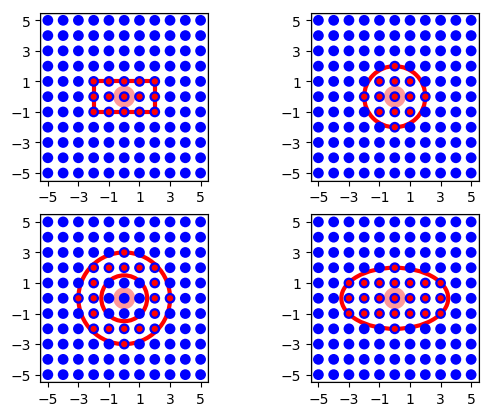
Figure 18 Masks for 2D layers. For all mask types, the driver node is marked by a wide light-red circle, the selected pool nodes by red dots and the masks by red lines. From left to right, top to bottom: rectangular, circular, doughnut and elliptical masks centered about the driver node.¶
By default, the masks are centered about the position of the driver
node, mapped into the pool layer. You can change the location of the
mask relative to the driver node by specifying an 'anchor' entry in
the mask dictionary. The anchor is a 2D vector specifying the location
of the mask center relative to the driver node, as in the following
examples (cf. Figure 19).
conndict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-2., -1.],
'upper_right': [2., 1.]},
'anchor': [-1.5, -1.5]}}
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 2.0},
'anchor': [-2.0, 0.0]}}
conndict = {'connection_type': 'divergent',
'mask': {'doughnut': {'inner_radius': 1.5,
'outer_radius': 3.},
'anchor': [1.5, 1.5]}}
conndict = {'connection_type': 'divergent',
'mask': {'elliptical': {'major_axis': 7.,
'minor_axis': 4.},
'anchor': [2.0, -1.0]}}
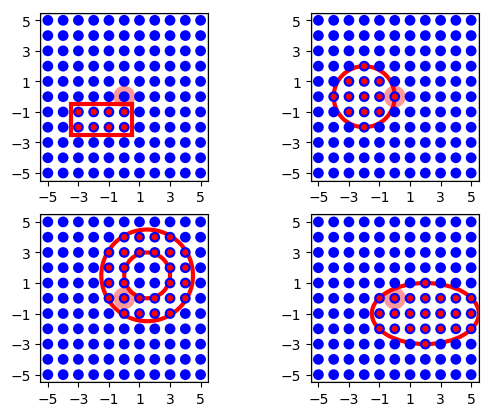
Figure 19 The same masks as in Figure 18, but centered about
\((-1.5,-1.5)\), \((-2,0)\), \((1.5,1.5)\) and
\((2, -1)\), respectively, using the 'anchor' parameter.¶
and \(\textbf{elliptical}\) masks, see Fig Figure 19. To do so,
add an 'azimuth_angle' entry in the specific mask dictionary. The
azimuth_angle is measured in degrees and is the rotational angle
from the x-axis to the y-axis.
conndict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-2., -1.],
'upper_right': [2., 1.],
'azimuth_angle': 120.}}}
conndict = {'connection_type': 'divergent',
'mask': {'elliptical': {'major_axis': 7.,
'minor_axis': 4.,
'azimuth_angle': 45.}}}
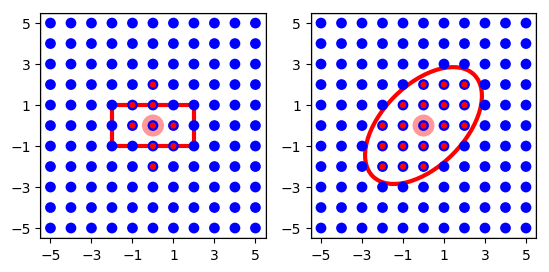
Figure 20 Rotated rectangle and elliptical mask from Figure 18 and Figure 19, where the rectangle mask is rotated \(120^\circ\) and the elliptical mask is rotated \(45^\circ\).¶
Similarly, there are three mask types that can be used for 3D layers,
- Box
All nodes within a cuboid volume are connected. The area is specified by its lower left and upper right corners, measured in the same unit as element coordinates. Example:
conndict = {'connection_type': 'divergent',
'mask': {'box': {'lower_left': [-2., -1., -1.],
'upper_right': [2., 1., 1.]}}}
- Spherical
All nodes within a sphere are connected. The area is specified by its radius.
conndict = {'connection_type': 'divergent',
'mask': {'spherical': {'radius': 2.5}}}
- Ellipsoidal
All nodes within an ellipsoid are connected. The area is specified by its major, minor, and polar axis. This mask has been part of NEST since NEST 2.14.
conndict = {'connection_type': 'divergent',
'mask': {'ellipsoidal': {'major_axis': 7.,
'minor_axis': 4.,
'polar_axis': 4.5}}}
As in the 2D case, you can change the location of the mask relative to
the driver node by specifying a 3D vector in the 'anchor' entry in
the mask dictionary. If you want to rotate the box or ellipsoidal masks,
you can add an 'azimuth_angle' entry in the specific mask dictionary
for rotation from the x-axis towards the y-axis about the z-axis, or an
'polar_angle' entry, specifying the rotation angle in degrees from
the z-axis about the (possibly rotated) x axis, from the (possibly
rotated) y-axis. You can specify both at once of course. If both are
specified, we first rotate about the z-axis and then about the new
x-axis. NEST currently do not support rotation in all three directions,
the rotation from the y-axis about the (possibly rotated) z-axis, from
the (possibly rotated) x-axis is missing.
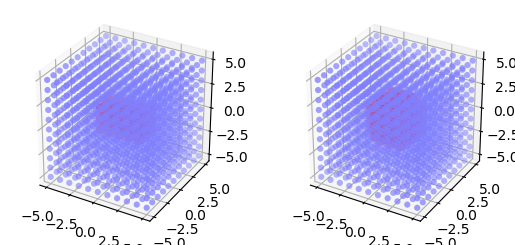
Figure 21 Masks for 3D layers. For all mask types, the driver node is marked by a wide light-red circle, the selected pool nodes by red dots and the masks by red lines. From left to right: box and spherical masks centered about the driver node.¶
Grid-based layers can be connected using rectangular grid masks. For these, you specify the size of the mask not by lower left and upper right corner coordinates, but give their size in rows and columns, as in this example:
conndict = {'connection_type': 'divergent',
'mask': {'grid': {'rows': 3, 'columns': 5}}}
The resulting connections are shown in Figure 22. By default the top-left corner of a grid mask, i.e., the grid mask element with grid index \([0,0]\) 4, is aligned with the driver node. You can change this alignment by specifying an anchor for the mask:
conndict = {'connection_type': 'divergent',
'mask': {'grid': {'rows': 3, 'columns': 5},
'anchor': {'row': 1, 'column': 2}}}
You can even place the anchor outside the mask:
conndict = {'connection_type': 'divergent',
'mask': {'grid': {'rows': 3, 'columns': 5},
'anchor': {'row': -1, 'column': 2}}}
The resulting connection patterns are shown in Figure 22.
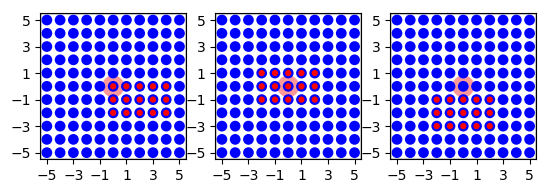
Figure 22 Grid masks for connections between grid-based layers. Left: \(5\times 3\) mask with default alignment at upper left corner. Center: Same mask, but anchored to center node at grid index \([1,2]\). Right: Same mask, but anchor to the upper left of the mask at grid index \([-1,2]\).¶
Connections specified using grid masks are generated more efficiently than connections specified using other mask types.
Note the following:
Grid-based masks are applied by considering grid indices. The position of nodes in physical coordinates is ignored.
In consequence, grid-based masks should only be used between layers with identical grid spacings.
The semantics of the
'anchor'property for grid-based masks differ significantly for general masks described in Sec. 3.3.1. For general masks, the anchor is the center of the mask relative to the driver node. For grid-based nodes, the anchor determines which mask element is aligned with the driver element.
Kernels¶
Many neuronal network models employ probabilistic connection rules. Topology supports probabilistic connections through kernels. A kernel is a function mapping the distance (or displacement) between a driver and a pool node to a connection probability. Topology then generates a connection according to this probability.
Probabilistic connections can be generated in two different ways using Topology:
- Free probabilistic connections
are the default. In this case,
ConnectLayersconsiders each driver node \(D\) in turn. For each \(D\), it evaluates the kernel for each pool node \(P\) within the mask and creates a connection according to the resulting probability. This means in particular that each possible driver-pool pair is inspected exactly once and that there will be at most one connection between each driver-pool pair.- Prescribed number of connections
can be obtained by specifying the number of connections to create per driver node. See Sec. 3.7 for details.
Available kernel functions are shown in Table tbl_kernels. More kernel functions may be created in a NEST extension module. This is covered in Chapter 5.
\(d\) is the distance and \((d_x,d_y)\) the displacement. All functions can be used to specify weights and delays, but only the constant and the distance-dependent functions, i.e., all functions above the double line, can be used as kernels.
Name
Parameters
Function
constantconstant \(p\in[0,1]\)
linear
a,c
exponential
a,c,tau
gausssian
p_center,sigma,mean,c
gaussian2D
p_center,sigma_x,sigma_y,mean_x,mean_y,rho,c
gamma
kappa,
theta
uniform
min,
max\(p\in [\text{min},\text{max})\) uniformly
normal
mean,sigma,min,max\(p \in [\text{min},\text{max})\) normal with given mean and \(\sigma\)
lognormal
mu,sigma,min,max\(p \in [\text{min},\text{max})\) lognormal with given \(\mu\) and \(\sigma\)
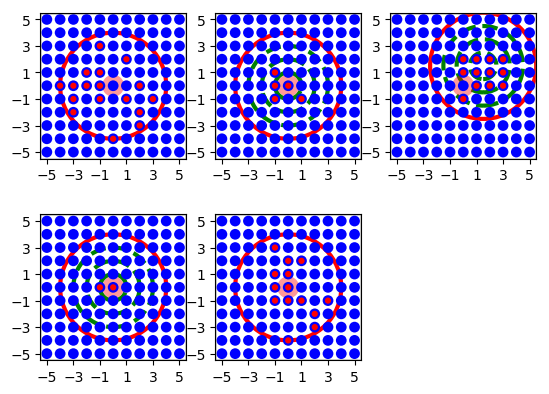
Figure 23 Illustration of various kernel functions. Top left: constant kernel, \(p=0.5\). Top center: Gaussian kernel, green dashed lines show \(\sigma\), \(2\sigma\), \(3\sigma\). Top right: Same Gaussian kernel anchored at \((1.5,1.5)\). Bottom left: Same Gaussian kernel, but all \(p<0.5\) treated as \(p=0\). Bottom center: 2D-Gaussian.¶
Several examples follow. They are illustrated in Figure 23.
- Constant
The simplest kernel is a fixed connection probability:
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 4.}},
'kernel': 0.5}
- Gaussian
This kernel is distance dependent. In the example, connection probability is 1 for \(d=0\) and falls off with a “standard deviation” of \(\sigma=1\):
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 4.}},
'kernel': {'gaussian': {'p_center': 1.0,
'sigma': 1.}}}
- Eccentric Gaussian
In this example, both kernel and mask have been moved using anchors:
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 4.},
'anchor': [1.5, 1.5]},
'kernel': {'gaussian': {'p_center': 1.0,
'sigma': 1.,
'anchor': [1.5, 1.5]}}}
Note that the anchor for the kernel is specified inside the dictionary containing the parameters for the Gaussian.
- Cut-off Gaussian
In this example, all probabilities less than \(0.5\) are set to zero:
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 4.}},
'kernel': {'gaussian': {'p_center': 1.0,
'sigma': 1.,
'cutoff': 0.5}}}
- 2D Gaussian
We conclude with an example using a two-dimensional Gaussian, i.e., a Gaussian with different widths in \(x\)- and \(y-\) directions. This kernel depends on displacement, not only on distance:
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 4.}},
'kernel': {'gaussian2D': {'p_center': 1.0,
'sigma_x': 1.,
'sigma_y': 3.}}}
Note that for pool layers with periodic boundary conditions, Topology always uses the shortest possible displacement vector from driver to pool neuron as argument to the kernel function.
Weights and delays¶
The functions presented in Table tbl_kernels can also be used to
specify distance-dependent or randomized weights and delays for the
connections created by ConnectLayers.
Figure Figure 24 illustrates weights and delays generated using these functions with the following code examples. All examples use a “layer” of 51 nodes placed on a line; the line is centered about \((25,0)\), so that the leftmost node has coordinates \((0,0)\). The distance between neighboring elements is 1. The mask is rectangular, spans the entire layer and is centered about the driver node.
Linear example
ldict = {'rows': 1, 'columns': 51,
'extent': [51., 1.], 'center': [25., 0.],
'elements': 'iaf_psc_alpha'}
cdict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-25.5, -0.5],
'upper_right': [25.5, 0.5]}},
'weights': {'linear': {'c': 1.0,
'a': -0.05,
'cutoff': 0.0}},
'delays': {'linear': {'c': 0.1, 'a': 0.02}}}
Results are shown in the top panel of Figure 24. Connection weights and delays are shown for the leftmost neuron as driver. Weights drop linearly from \(1\). From the node at \((20,0)\) on, the cutoff sets weights to 0. There are no connections to nodes beyond \((25,0)\), since the mask extends only 25 units to the right of the driver. Delays increase in a stepwise linear fashion, as NEST requires delays to be multiples of the simulation resolution.
Linear example with periodic boundary conditions
cdict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-25.5, -0.5],
'upper_right': [25.5, 0.5]}},
'weights': {'linear': {'c': 1.0,
'a': -0.05,
'cutoff': 0.0}},
'delays': {'linear': {'c': 0.1, 'a': 0.02}}}
Results are shown in the middle panel of Figure 24. This example is identical to the previous, except that the (pool) layer has periodic boundary conditions. Therefore, the left half of the mask about the node at \((0,0)\) wraps back to the right half of the layer and that node connects to all nodes in the layer.
Various functions
cdict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-25.5, -0.5],
'upper_right': [25.5, 0.5]}},
'weights': {'exponential': {'a': 1., 'tau': 5.}}}
cdict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-25.5, -0.5],
'upper_right': [25.5, 0.5]}},
'weights': {'gaussian': {'p_center': 1., 'sigma': 5.}}}
Results are shown in the bottom panel of Figure 24. It shows linear, exponential and Gaussian weight functions for the node at \((25,0)\).
Randomized weights and delays
cdict = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-25.5, -0.5],
'upper_right': [25.5, 0.5]}},
'weights': {'uniform': {'min': 0.2, 'max': 0.8}}}
By using the 'uniform' function for weights or delays, one can
obtain randomized values for weights and delays, as shown by the red
circles in the bottom panel of Figure 24. Weights and delays can
currently only be randomized with uniform distribution.
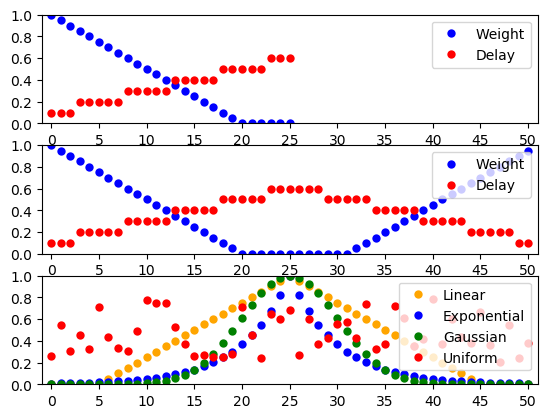
Figure 24 Distance-dependent and randomized weights and delays. See text for details.¶
Periodic boundary conditions¶
Connections between layers with periodic boundary conditions are based on the following principles:
Periodic boundary conditions are always applied in the pool layer. It is irrelevant whether the driver layer has periodic boundary conditions or not.
By default, Topology does not accept masks that are wider than the pool layer when using periodic boundary conditions. Otherwise, one pool node could appear as multiple targets to the same driver node as the masks wraps several times around the layer. For layers with different extents in \(x\)- and \(y\)-directions this means that the maximum layer size is determined by the smaller extension.
Kernel, weight and delay functions always consider the shortest distance (displacement) between driver and pool node.
In most physical systems simulated using periodic boundary conditions, interactions between entities are short-range. Periodic boundary conditions are well-defined in such cases. In neuronal network models with long-range interactions, periodic boundary conditions may not make sense. In general, we recommend to use periodic boundary conditions only when connection masks are significantly smaller than the layers they are applied to.
Prescribed number of connections¶
We have so far described how to connect layers by either connecting to all nodes inside the mask or by considering each pool node in turn and connecting it according to a given probability function. In both cases, the number of connections generated depends on mask and kernel.
Many neuron models in the literature, in contrast, prescribe a certain fan in (number of incoming connections) or fan out (number of outgoing connections) for each node. You can achieve this in Topology by prescribing the number of connections for each driver node. For convergent connections, where the target layer is the driver layer, you thus achieve a constant fan in, for divergent connections a constant fan out.
Connection generation now proceeds in a different way than before:
For each driver node,
ConnectLayersrandomly selects a node from the mask region in the pool layer, and creates a connection with the probability prescribed by the kernel. This is repeated until the requested number of connections has been created.Thus, if all nodes in the mask shall be connected with equal probability, you should not specify any kernel.
If you specify a non-uniform kernel (e.g., Gaussian, linear, exponential), the connections will be distributed within the mask with the spatial profile given by the kernel.
If you prohibit multapses (cf Sec. 3.1.1) and prescribe a number of connections greater than the number of pool nodes in the mask,
ConnectLayersmay get stuck in an infinite loop and NEST will hang. Keep in mind that the number of nodes within the mask may vary considerably for free layers with randomly placed nodes.
The following code generates a network of 1000 randomly placed nodes and connects them with a fixed fan out of 50 outgoing connections per node distributed with a profile linearly decaying from unit probability to zero probability at distance \(0.5\). Multiple connections (multapses) between pairs of nodes are allowed, self-connections (autapses) prohibited. The probability of finding a connection at a certain distance is then given by the product of the probabilities for finding nodes at a certain distance with the kernel value for this distance. For the kernel and parameter values below we have
The resulting distribution of distances between connected nodes is shown in Figure 25.
pos = [[np.random.uniform(-1., 1.), np.random.uniform(-1., 1.)]
for j in range(1000)]
ldict = {'positions': pos, 'extent': [2., 2.],
'elements': 'iaf_psc_alpha', 'edge_wrap': True}
cdict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 1.0}},
'kernel': {'linear': {'c': 1., 'a': -2., 'cutoff': 0.0}},
'number_of_connections': 50,
'allow_multapses': True, 'allow_autapses': False}
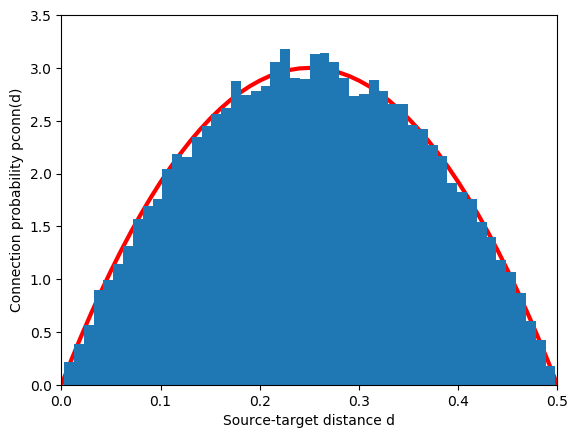
Figure 25 Distribution of distances between source and target for a network of
1000 randomly placed nodes, a fixed fan out of 50 connections and a
connection probability decaying linearly from 1 to 0 at
\(d=0.5\). The red line is the expected distribution from
Eq. eq_ptheo.¶
Functions determining weight and delay as function of distance/displacement work in just the same way as before when the number of connections is prescribed.
Connecting composite layers¶
Connections between layers with composite elements are based on the following principles:
All nodes within a composite element have the same coordinates, the coordinates of the element.
All nodes within a composite element are treated equally. If, e.g., an element of the pool layer contains three nodes and connection probability is 1, then connections with all three nodes will be created. For probabilistic connection schemes, each of the three nodes will be considered individually.
If only nodes of a given model within each element shall be considered as sources or targets then this can be achieved by adding a
'sources'or'targets'entry to the connection dictionary, which specifies the model to connect.
This is exemplified by the following code, which connects pyramidal
cells (pyr) to interneurons (in) with a circular mask and
uniform probability and interneurons to pyramidal cells with a
rectangular mask unit probability.
nest.ResetKernel()
nest.CopyModel('iaf_psc_alpha', 'pyr')
nest.CopyModel('iaf_psc_alpha', 'in')
ldict = {'rows': 10, 'columns': 10, 'elements': ['pyr', 'in']}
cdict_p2i = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 0.5}},
'kernel': 0.8,
'sources': {'model': 'pyr'},
'targets': {'model': 'in'}}
cdict_i2p = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-0.2, -0.2],
'upper_right': [0.2, 0.2]}},
'sources': {'model': 'in'},
'targets': {'model': 'pyr'}}
l = tp.CreateLayer(ldict)
tp.ConnectLayers(l, l, cdict_p2i)
tp.ConnectLayers(l, l, cdict_i2p)
Synapse models and properties¶
By default, ConnectLayers creates connections using the default
synapse model in NEST, static_synapse. You can specify a different
model by adding a 'synapse_model' entry to the connection
dictionary, as in this example:
nest.ResetKernel()
nest.CopyModel('iaf_psc_alpha', 'pyr')
nest.CopyModel('iaf_psc_alpha', 'in')
nest.CopyModel('static_synapse', 'exc', {'weight': 2.0})
nest.CopyModel('static_synapse', 'inh', {'weight': -8.0})
ldict = {'rows': 10, 'columns': 10, 'elements': ['pyr', 'in']}
cdict_p2i = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 0.5}},
'kernel': 0.8,
'sources': {'model': 'pyr'},
'targets': {'model': 'in'},
'synapse_model': 'exc'}
cdict_i2p = {'connection_type': 'divergent',
'mask': {'rectangular': {'lower_left': [-0.2, -0.2],
'upper_right': [0.2, 0.2]}},
'sources': {'model': 'in'},
'targets': {'model': 'pyr'},
'synapse_model': 'inh'}
l = tp.CreateLayer(ldict)
tp.ConnectLayers(l, l, cdict_p2i)
tp.ConnectLayers(l, l, cdict_i2p)
You have to use synapse models if you want to set, e.g., the receptor type of connections or parameters for plastic synapse models. These can not be set in distance-dependent ways at present.
Connecting devices to subregions of layers¶
It is possible to connect stimulation and recording devices only to specific subregions of layers. A simple way to achieve this is to create a layer which contains only the device placed typically in its center. For connecting the device layer to a neuron layer, an appropriate mask needs to be specified and optionally also an anchor for shifting the center of the mask. As demonstrated in the following example, stimulation devices require the divergent connection type
nrn_layer = tp.CreateLayer({'rows': 20,
'columns': 20,
'elements': 'iaf_psc_alpha'})
stim = tp.CreateLayer({'rows': 1,
'columns': 1,
'elements': 'poisson_generator'})
cdict_stim = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 0.1},
'anchor': [0.2, 0.2]}}
tp.ConnectLayers(stim, nrn_layer, cdict_stim)
while recording devices require the convergent connection type (see also Sec. 3.11):
rec = tp.CreateLayer({'rows': 1,
'columns': 1,
'elements': 'spike_detector'})
cdict_rec = {'connection_type': 'convergent',
'mask': {'circular': {'radius': 0.1},
'anchor': [-0.2, 0.2]}}
tp.ConnectLayers(nrn_layer, rec, cdict_rec)
Layers and recording devices¶
Generally, one should not create a layer of recording devices, especially spike detectors, to record from a topology layer. Instead, create a single spike detector, and connect all neurons in the layer to that spike detector using a normal connect command:
rec = nest.Create('spike_detector')
nrns = nest.GetLeaves(nrn_layer, local_only=True)[0]
nest.Connect(nrns, rec)
Connections to a layer of recording devices as described in Sec. 3.10, such as spike detectors, are only possible using the convergent connection type without a fixed number of connections. Note that voltmeter and multimeter are not suffering from this restriction, since they are connected as sources, not as targets.
Inspecting Layers¶
We strongly recommend that you inspect the layers created by Topology to be sure that node placement and connectivity indeed turned out as expected. In this chapter, we describe some functions that NEST and Topology provide to query and visualize networks, layers, and connectivity.
Query functions¶
The following table presents some query functions provided by NEST
(nest.) and Topology (tp.). For detailed information about these
functions, please see the online Python and SLI documentation.
|
Print structure of network or subnet from NEST perspective. |
|
Retrieve connections (all or for a given source or target); see also http://www.nest-simulator.org/connection_ma nagement. |
|
Applied to a layer, returns GIDs of the layer elements. For simple layers, these are the actual model neurons, for composite layers the top-level subnets. |
|
Applied to a layer, returns GIDs of all actual model neurons, ignoring subnets. |
|
Return the spatial locations of nodes. |
|
Return the layer to which nodes belong. |
|
Return the node(s) at the location(s) in the given grid-based layer(s). |
|
Obtain targets of a list of sources in a given target layer. |
|
Obtain positions of targets of a list of sources in a given target layer. |
|
Return the node(s) closest to the location(s) in the given layer(s). |
|
Return GID(s) of node closest to center of layer(s). |
|
Obtain vector of lateral displacement between nodes, taking periodic boundary conditions into account. |
|
Obtain vector of lateral distances between nodes, taking periodic boundary conditions into account. |
|
Write layer element positions to file. |
|
Write connectivity information to file. This function may be very useful to check that Topology created the correct connection structure. |
|
Obtain GIDs of nodes/elements inside a masked area of a layer. Part of NEST since NEST 2.14. |
Visualization functions¶
Topology provides three functions to visualize networks:
|
Plot nodes in a layer. |
|
Plot all targets of a node in a given layer. |
|
Add indication of mask and kernel to
plot of layer. It does not wrap masks
and kernels with respect to periodic
boundary conditions. This function is
usually called by |
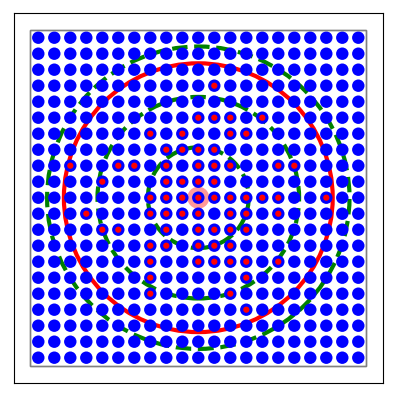
Figure 26 \(21\times 21\) grid with divergent Gaussian projections onto itself. Blue circles mark layer elements, red circles connection targets of the center neuron (marked by large light-red circle). The large red circle is the mask, the dashed green lines mark \(\sigma\), \(2\sigma\) and \(3\sigma\) of the Gaussian kernel.¶
The following code shows a practical example: A \(21\times21\) network which connects to itself with divergent Gaussian connections. The resulting graphics is shown in Figure 26. All elements and the targets of the center neuron are shown, as well as mask and kernel.
l = tp.CreateLayer({'rows': 21, 'columns': 21,
'elements': 'iaf_psc_alpha'})
conndict = {'connection_type': 'divergent',
'mask': {'circular': {'radius': 0.4}},
'kernel': {'gaussian': {'p_center': 1.0, 'sigma': 0.15}}}
tp.ConnectLayers(l, l, conndict)
fig = tp.PlotLayer(l, nodesize=80)
ctr = tp.FindCenterElement(l)
tp.PlotTargets(ctr, l, fig=fig,
mask=conndict['mask'], kernel=conndict['kernel'],
src_size=250, tgt_color='red', tgt_size=20,
kernel_color='green')
Adding topology kernels and masks¶
This chapter will show examples of how to extend the topology module by adding custom kernel functions and masks. Some knowledge of the C++ programming language is needed for this. The functions will be added as a part of an extension module which is dynamically loaded into NEST. For more information on writing an extension module, see the section titled “Writing an Extension Module” in the NEST Developer Manual. The basic steps required to get started are:
From the NEST source directory, copy directory examples/MyModule to somewhere outside the NEST source, build or install directories.
Change to the new location of MyModule and prepare by issuing
./bootstrap.shLeave MyModule and create a build directory for it, e.g., mmb next to it
cd .. mkdir mmb cd mmb
Configure. The configure process uses the script
nest-configto find out where NEST is installed, where the source code resides, and which compiler options were used for compiling NEST. Ifnest-configis not in your path, you need to provided it explicitly like thiscmake -Dwith-nest=${NEST_INSTALL_DIR}/bin/nest-config ../MyModule
MyModule will then be installed to
\${NEST_INSTALL_DIR}. This ensures that NEST will be able to find initializing SLI files for the module. You should not use the--prefixto select a different installation destination. If you do, you must make sure to use addpath in SLI before loading the module to ensure that NEST will find the SLI initialization file for your module.Compile.
make make install
The previous command installed MyModule to the NEST installation directory, including help files generated from the source code.
Adding kernel functions¶
As an example, we will add a kernel function called 'affine2d',
which will be linear (actually affine) in the displacement of the nodes,
on the form
The kernel functions are provided by C++ classes subclassed from
nest::Parameter. To enable subclassing, add the following lines at
the top of the file mymodule.h:
#include "topologymodule.h"
#include "parameter.h"
Then, add the class definition, e.g. near the bottom of the file before
the brace closing the namespace mynest:
class Affine2DParameter: public nest::Parameter
{
public:
Affine2DParameter(const DictionaryDatum& d):
Parameter(d),
a_(1.0),
b_(1.0),
c_(0.0)
{
updateValue<double>(d, "a", a_);
updateValue<double>(d, "b", b_);
updateValue<double>(d, "c", c_);
}
double raw_value(const nest::Position<2>& disp,
librandom::RngPtr&) const
{
return a_*disp[0] + b_*disp[1] + c_;
}
nest::Parameter * clone() const
{ return new Affine2DParameter(*this); }
private:
double a_, b_, c_;
};
The class contains a constructor, which reads the value of the
parameters \(a\), \(b\) and \(c\) from the dictionary
provided by the user. The function updateValue will do nothing if
the given key is not in the dictionary, and the default values
\(a=b=1,\ c=0\) will be used.
The overridden method raw_value() will return the actual value of
the kernel function for the displacement given as the first argument,
which is of type nest::Position<2>. The template argument 2 refers
to a 2-dimensional position. You can also implement a method taking a
nest::Position<3> as the first argument if you want to support
3-dimensional layers. The second argument, a random number generator, is
not used in this example.
The class also needs to have a clone() method, which will return a
dynamically allocated copy of the object. We use the (default) copy
constructor to implement this.
To make the custom function available to the Topology module, you need to register the class you have provided. To do this, add the line
nest::TopologyModule::register_parameter<Affine2DParameter>("affine2d");
to the function MyModule::init() in the file mymodule.cpp. Now
compile and install the module by issuing
make
make install
To use the function, the module must be loaded into NEST using
nest.Install(). Then, the function is available to be used in
connections, e.g.
nest.Install('mymodule')
l = tp.CreateLayer({'rows': 11, 'columns': 11, 'extent': [1.,1.],
'elements': 'iaf_psc_alpha'})
tp.ConnectLayers(l,l,{'connection_type': 'convergent',
'mask': {'circular': {'radius': 0.5}},
'kernel': {'affine2d': {'a': 1.0, 'b': 2.0, 'c': 0.5}}})
Adding masks¶
The process of adding a mask is similar to that of adding a kernel
function. A subclass of nest::Mask<D> must be defined, where D
is the dimension (2 or 3). In this case we will define a 2-dimensional
elliptic mask by creating a class called EllipticMask. Note that
elliptical masks are already part of NEST see
Sec. 3.3. That elliptical mask is defined in a
different way than what we will do here though, so this can still be
used as an introductory example. First, we must include another header
file:
#include "mask.h"
Compared to the Parameter class discussed in the previous section,
the Mask class has a few more methods that must be overridden:
class EllipticMask : public nest::Mask<2>
{
public:
EllipticMask(const DictionaryDatum& d):
rx_(1.0), ry_(1.0)
{
updateValue<double>(d, "r_x", rx_);
updateValue<double>(d, "r_y", ry_);
}
using Mask<2>::inside;
// returns true if point is inside the ellipse
bool inside(const nest::Position<2> &p) const
{ return p[0]*p[0]/rx_/rx_ + p[1]*p[1]/ry_/ry_ <= 1.0; }
// returns true if the whole box is inside the ellipse
bool inside(const nest::Box<2> &b) const
{
nest::Position<2> p = b.lower_left;
// Test if all corners are inside mask
if (not inside(p)) return false; // (0,0)
p[0] = b.upper_right[0];
if (not inside(p)) return false; // (0,1)
p[1] = b.upper_right[1];
if (not inside(p)) return false; // (1,1)
p[0] = b.lower_left[0];
if (not inside(p)) return false; // (1,0)
return true;
}
// returns bounding box of ellipse
nest::Box<2> get_bbox() const
{
nest::Position<2> ll(-rx_,-ry_);
nest::Position<2> ur(rx_,ry_);
return nest::Box<2>(ll,ur);
}
nest::Mask<2> * clone() const
{ return new EllipticMask(*this); }
protected:
double rx_, ry_;
};
The overridden methods include a test if a point is inside the mask, and for efficiency reasons also a test if a box is fully inside the mask. We implement the latter by testing if all the corners are inside, since our elliptic mask is convex. We must also define a function which returns a bounding box for the mask, i.e. a box completely surrounding the mask.
Similar to kernel functions, the mask class must be registered with the
topology module, and this is done by adding a line to the function
MyModule::init() in the file mymodule.cpp:
nest::TopologyModule::register_mask<EllipticMask>("elliptic");
After compiling and installing the module, the mask is available to be used in connections, e.g.
nest.Install('mymodule')
l = tp.CreateLayer({'rows': 11, 'columns': 11, 'extent': [1.,1.],
'elements': 'iaf_psc_alpha'})
tp.ConnectLayers(l,l,{'connection_type': 'convergent',
'mask': {'elliptic': {'r_x': 0.5, 'r_y': 0.25}}})
Changes between versions¶
In this chapter we give summaries of the most important changes in the Topology Module between different NEST versions, starting with the most recent ones.
Changes from Topology 2.14 to 2.16¶
The one important change in the Topology module from NEST version 2.14 to 2.16 was the inclusion of rotated masks:
Rotation of
rectangular/boxandelliptical/ellipsoidalmasks is now possible. NEST offers rotation in two directions, from the x-axis towards the y-axis, and from the z-axis away from the y-axis. To specify the former use the variableazimuth_angleand for the latter, usepolar_angle.
Changes from Topology 2.12 to 2.14¶
This is a short summary of the most important changes in the Topology Module from NEST version 2.12 to 2.14.
Elliptical and ellipsoidal masks have been added to NEST with NEST 2.14. To specify the mask, the
major_axis,minor_axisand (for ellipsoidal masks)polar_axismust be specified.It is now possible to obtain the GIDs inside a masked area with the function SelectNodesByMask.
Changes from Topology 2.0 to 2.2¶
This is a short summary of the most important changes in the Topology Module from NEST version 2.0 to 2.2.
Nested layers are no longer supported.
Subnets are no longer used inside composite layers. A call to GetElement for a composite layer will now return a list of GIDs for the nodes at the position rather than a single subnet GID.
Positions in layers may now be 3-dimensional.
The functions GetPosition, Displacement and Distance now only works for nodes local to the current MPI process, if used in a MPI-parallel simulation.
It is now possible to add kernel functions and masks to the Topology module through an extension module. Please see Chapter 5 for examples.
Changes from Topology 1.9 to 2.0¶
This is a short summary of the most important changes in the NEST Topology Module from the 1.9-xxxx to the 2.0 version.
ConnectLayer is now called ConnectLayers
Several other functions changed names, and there are many new functions. Please see Ch. 4 for an overview.
All nest.topology functions now require lists of GIDs as input, not “naked” GIDs
There are a number of new functions in nest.topology, I tried to write good doc strings for them
For grid based layers (ie those with /rows and /columns), we have changed the definition of “extent”: Previously, nodes were placed on the edges of the extent, so if you had an extend of 2 (in x-direction) and 3 nodes, these had x-coordinates -1, 0, 1. The grid constant was extent/(num_nodes - 1).
Now, we define the grid constant as extent/num_nodes, center the nodes about 0 and thus add a space of half a grid constant between the outermost nodes and the boundary of the extent. If you want three nodes at -1,0,1 you thus have to set the extent to 3, i.e., stretching from -1.5 to 1.5.
The main reason for this change was that topology always added this padding silently when you used periodic boundary conditions (otherwise, neurons are the left and right edge would have been in identical locations, not what one wants).
The semantics of the
anchorentry for kernel functions has changed: the anchor now specifies the center of the probability distribution relative to the driver node. This is consistent with the semantics for free masks, see Sec. 3.3 and 3.4.Functions computing connection probabilities, weights and delays as functions of distance between source and target nodes now handle periodic boundary conditions correctly.
Masks with a diameter larger than the diameter of the layer they are applied to are now prohibited by default. This avoids multiple connections when masks overwrap.
References¶
- 1
NEST is available under an open source license at www.nest-simulator.org.
- 2
See Nord (2009) for suggestions on how to describe network models.
- 3
You can also use standard NEST connection functions to connect nodes in Topology layers.
- 4
See Sec. 2.1.1 for the distinction between layer coordinates and grid indices