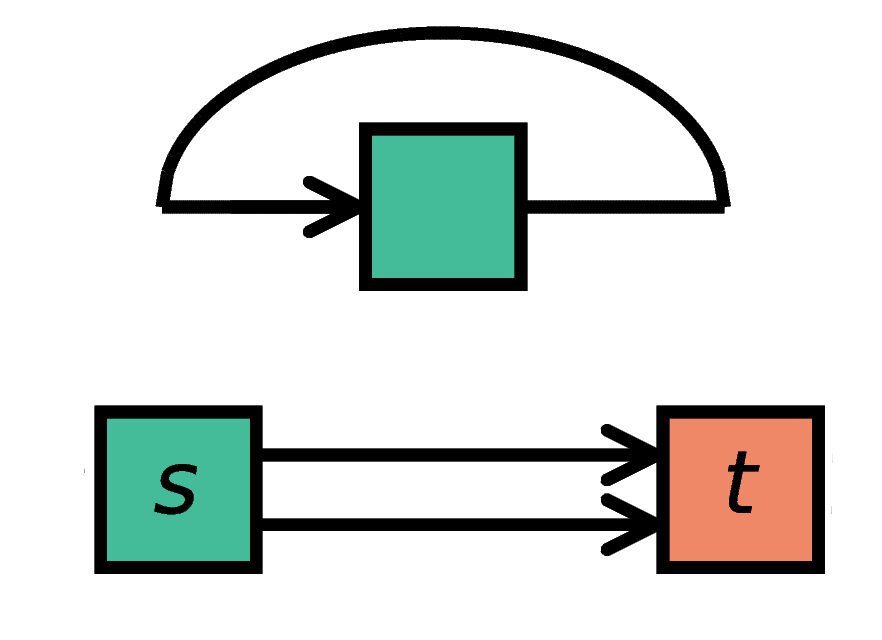
Connectivity concepts¶
Basic connection rules commonly used in the computational neuroscience community. For more details, go to the section Connection rules or just click on one of the illustrations.
This documentation not only describes how to define network connectivity in NEST, but also provides details on connectivity concepts. The article “Connectivity concepts in neuronal network modeling” [1] serves as a permanent reference for a number of connection rules and we suggest to cite it if rules defined there are used. This documentation instead represents a living reference for these rules, and deviations from and extensions to what is described in the article will be highlighted.
The same article also introduces a graphical notation for neuronal network diagrams which is curated in the documentation of NEST Desktop.
Spatially-structured networks are described on a separate page.
We use the term connection to mean a single, atomic edge between network nodes (i.e., neurons or devices). A projection is a group of edges that connects groups of nodes with similar properties (i.e., populations). To specify network connectivity, each projection is specified by a triplet of source population, target population, and a connection rule which defines how to connect the individual nodes.
Projections are created in NEST with the Connect() function:
nest.Connect(pre, post)
nest.Connect(pre, post, conn_spec)
nest.Connect(pre, post, conn_spec, syn_spec)
In the simplest case, the function just takes the NodeCollections pre and post, defining the nodes of
origin (sources) and termination (targets) for the connections to be established with the default rule all-to-all and the synapse model static_synapse.
Other connectivity patterns can be achieved by explicitly specifying the connection rule with the connectivity specification dictionary conn_spec which expects a rule alongside additional rule-specific parameters.
Rules that do not require parameters can be directly provided as string instead of the dictionary; for example, nest.Connect(pre, post, 'one_to_one').
Examples of parameters might be in- and out-degrees, or the probability for establishing a connection.
All available rules are described in the section Connection rules below.
Properties of individual connections (i.e., synapses) can be set via the synapse specification dictionary syn_spec.
Parameters like the synaptic weight or delay can be either set values or drawn and combined flexibly from random distributions.
For details on synapse models and their parameters refer to Synapse specification. Note that is also possible to define multiple projections with different synapse properties in the same Connect() call (see Collocated synapses).
By using the keyword variant nest.Connect(pre, post, syn_spec=syn_spec), the conn_spec can be omitted in the call to Connect() and will just take on the default value all-to-all.
After your connections are established, a quick sanity check is to look up the number of connections in the network, which can be easily done using the corresponding kernel attribute:
print(nest.num_connections)
Have a look at the section Working with connections to get more tips on how to examine the connections in greater detail.
Connection rules¶
Here we elaborate on the connectivity concepts with details on Autapses and multapses, Deterministic connection rules, Probabilistic connection rules, and the Connection generator interface (a method to create connections via CSA, the Connection Set Algebra [2]).
Finally, we introduce the rule Tripartite Bernoulli with pool for third-party connections in addition to primary connections between pre and post.
Each primary rule is described with an illustration, a NEST code example, and mathematical details.
The mathematical details are extracted from the study on connectivity concepts [1] and contain a symbol which we recommend to use for describing this type of connectivity, the corresponding expression from CSA, and a formal definition with an algorithmic construction rule and the resulting connectivity distribution.
Mathematical details: General notations and definitions
Autapses and multapses¶
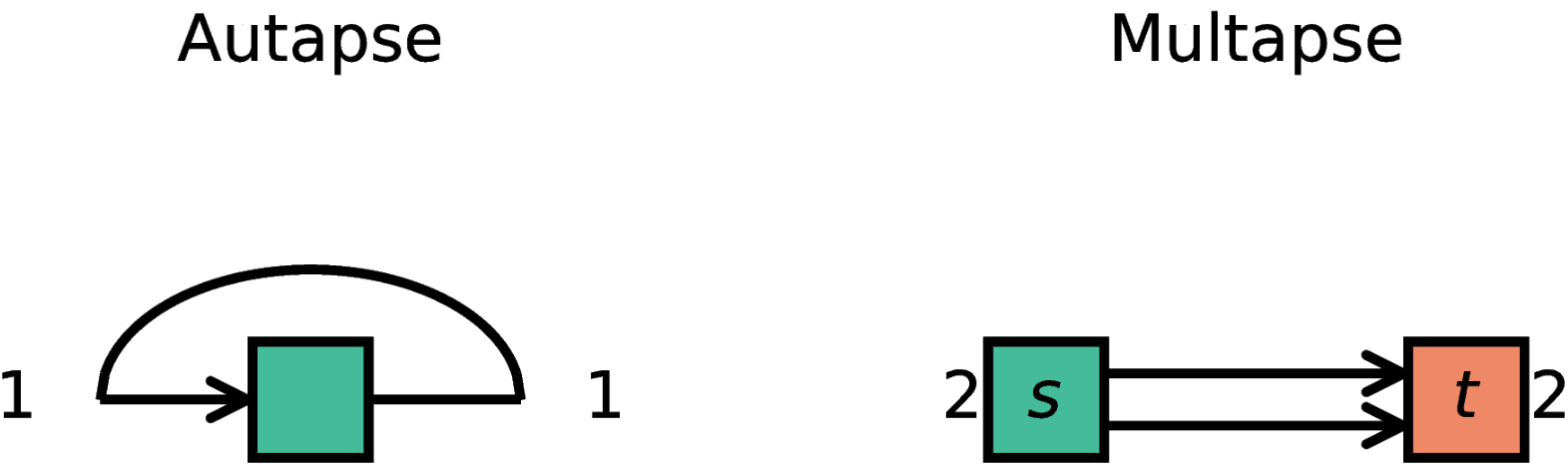
Autapses are self-connections of a node and multapses are multiple connections betweeen the same pair of nodes.
In the connection specification dictionary conn_spec, the additional switches allow_autapses (default:
True) and allow_multapses (default: True) can be set to allow or disallow autapses and multapses.
These switches are only effective during each single call to
Connect(). Calling the function multiple times with the same set of
neurons might still lead to violations of these constraints, even though the
switches were set to False in each individual call.
Deterministic connection rules¶
Deterministic connection rules establish precisely defined sets of connections without any variability across network realizations.
One-to-one¶
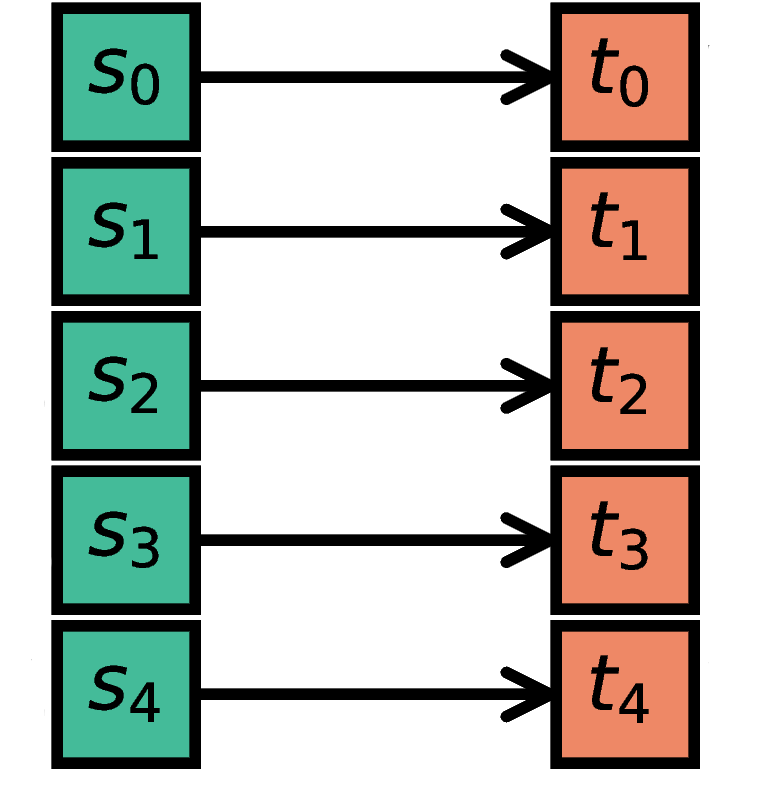
The i-th node in S (source) is connected to the i-th node in T (target). The
NodeCollections of S and T have to contain the same number of
nodes.
n = 5
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('spike_recorder', n)
nest.Connect(S, T, 'one_to_one')
Mathematical details: One-to-one
All-to-all¶
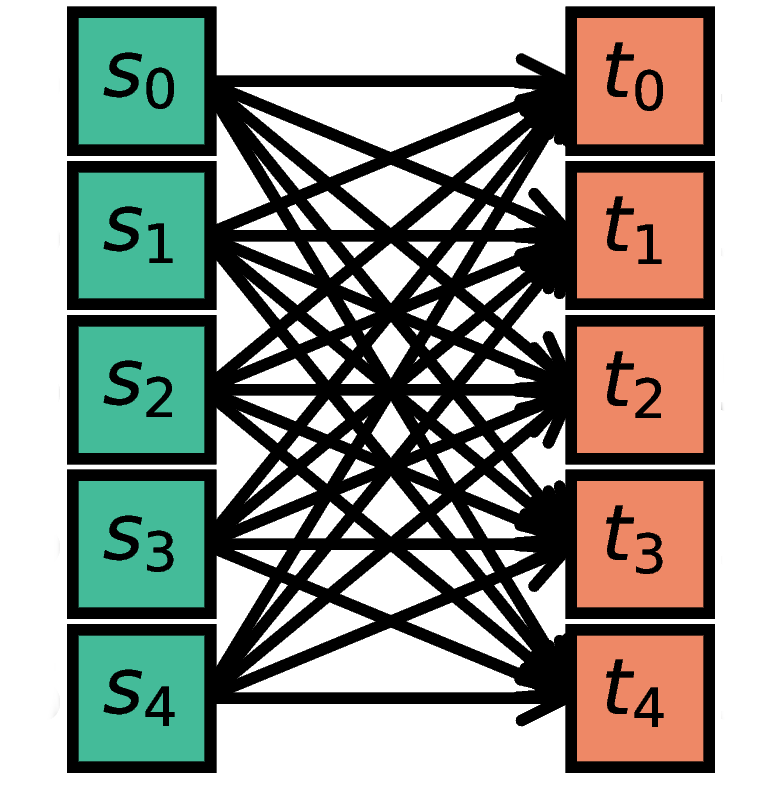
Each node in S is connected to every node in T. Since
all_to_all is the default, the rule doesn’t actually have to be
specified.
n, m = 5, 5
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('iaf_psc_alpha', m)
nest.Connect(S, T, 'all_to_all')
nest.Connect(S, T) # equivalent
Mathematical details: All-to-all
Explicit connections¶
Connections between explicit lists of source-target pairs can be realized in NEST by extracting the respective node ids from the NodeCollections and using the One-to-one rule.
n, m = 5, 5
S = nest.Create('iaf_psc_alpha', n) # node ids: 1..5
T = nest.Create('iaf_psc_alpha', m) # node ids: 6..10
# source-target pairs: (3,8), (4,1), (1,9)
nest.Connect([3,4,1], [8,6,9], 'one_to_one')
Mathematical details: Explicit connections
Probabilistic connection rules¶
Probabilistic connection rules establish edges according to a probabilistic rule. Consequently, the exact connectivity varies with realizations. Still, such connectivity leads to specific expectation values of network characteristics, such as degree distributions or correlation structure.
Pairwise Bernoulli¶
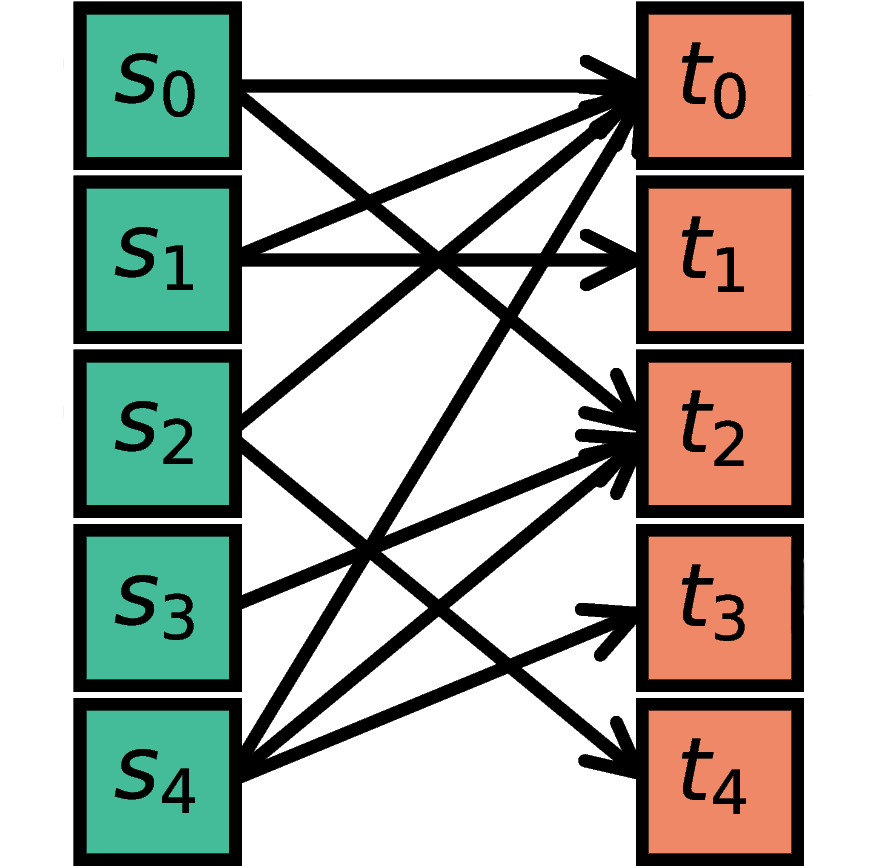
For each possible pair of nodes from S and T, a connection is
created with probability p.
Note that multapses cannot be produced with this rule because each possible edge is visited only once, independent of how allow_multapses is set.
n, m, p = 5, 5, 0.5
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('iaf_psc_alpha', m)
conn_spec = {'rule': 'pairwise_bernoulli', 'p': p}
nest.Connect(S, T, conn_spec)
Mathematical details: Pairwise Bernoulli
and
respectively. The expected total number of edges equals \(\text{E}[N_\text{syn}]=pN_tN_s\).
Symmetric pairwise Bernoulli¶
For each possible pair of nodes from S and T, a connection is
created with probability p from S to T, as well as a
connection from T to S (two connections in total). To use
this rule, allow_autapses must be False, and make_symmetric
must be True.
n, m, p = 10, 12, 0.2
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('iaf_psc_alpha', m)
conn_spec = {'rule': 'symmetric_pairwise_bernoulli', 'p': p,
'allow_autapses': False, 'make_symmetric': True}
nest.Connect(S, T, conn_spec)
Pairwise Poisson¶
For each possible pair of nodes from S and T, a number of
connections is created following a Poisson distribution with mean
pairwise_avg_num_conns. This means that even for a small
average number of connections between single neurons in S and
T multiple connections are possible. Thus, for this rule
allow_multapses cannot be False.
The pairwise_avg_num_conns can be greater than one.
n, m, p_avg_num_conns = 10, 12, 0.2
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('iaf_psc_alpha', m)
conn_spec = {'rule': 'pairwise_poisson',
'pairwise_avg_num_conns': p_avg_num_conns}
nest.Connect(S, T, conn_spec)
Random, fixed total number¶
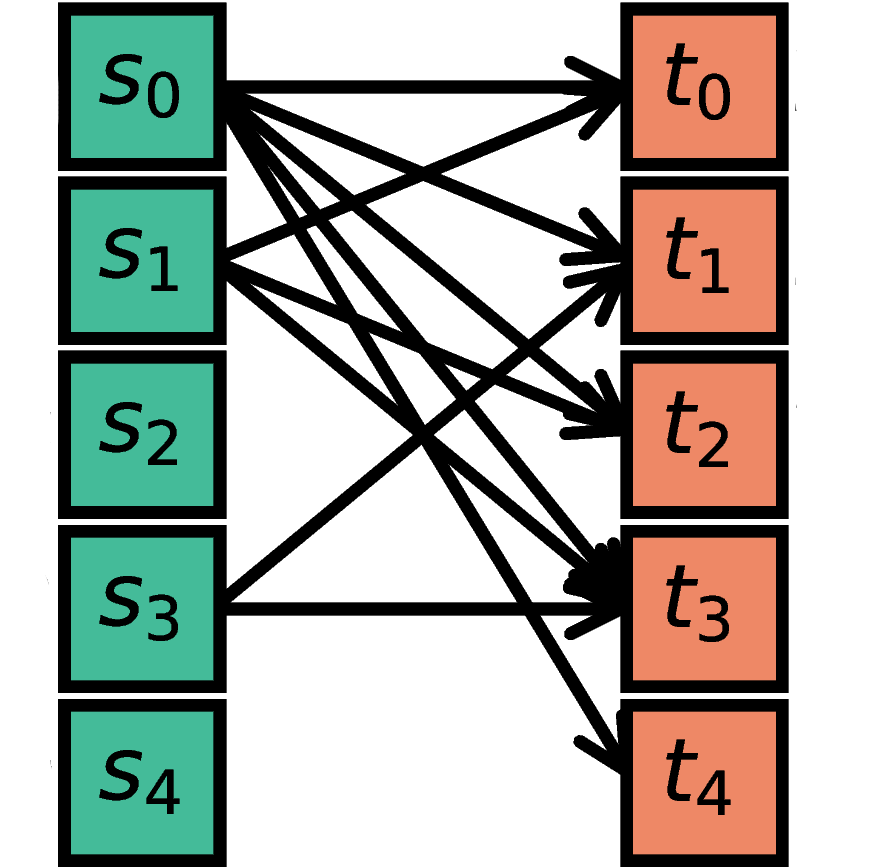
The nodes in S are randomly connected with the nodes in T
such that the total number of connections equals N.
As multapses are per default allowed and possible with this rule, you can disallow them by adding 'allow_multapses': False to the conn_dict.
n, m, N = 5, 5, 10
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('iaf_psc_alpha', m)
conn_spec = {'rule': 'fixed_total_number', 'N': N}
nest.Connect(S, T, conn_spec)
Mathematical details: Random, fixed total number with multapses
with \(p=1/N_t\).
The out-degrees have an analogous multinomial distribution \(P(K_{\text{out},1}=K_1,\ldots,K_{\text{out},N_s}=K_{N_s})\), with \(p=1/N_s\) and sources and targets switched. The marginal distributions are binomial distributions \(P(K_{\text{in},j}=K)= \mathcal{B}(K|N_\text{syn},1/N_t)\) and \(P(K_{\text{out},j}=K)= \mathcal{B}(K|N_\text{syn},1/N_s)\), respectively.
The \(\mathbf{M}\)-operator of CSA should not be confused with the “\(M\)” indicating that multapses are allowed in our symbolic notation.
Mathematical details: Random, fixed total number without multapses
and analogously \(P(K_{\text{out},1}=K_1,\ldots,K_{\text{out},N_s}=K_{N_s})\) with \(K_\text{out}\) instead of \(K_\text{in}\) and source and target indices switched.
The marginal distributions, i.e., the probability distribution for any specific node \(j\) to have in-degree \(K_j\), are hypergeometric distributions
with sources and targets switched for \(P(K_{\text{out},j}=K_j)\).
Random, fixed in-degree¶
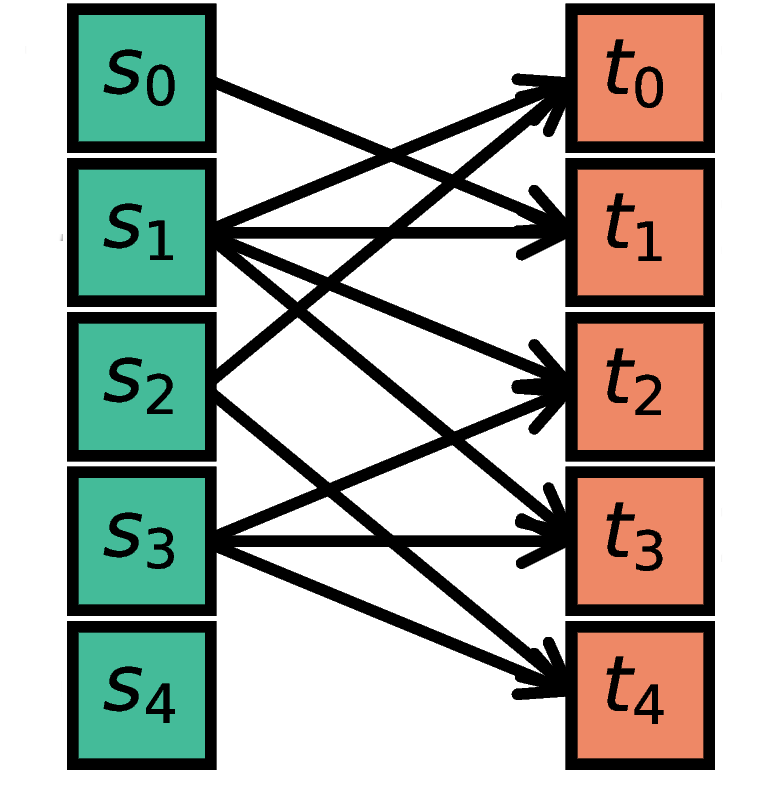
The nodes in S are randomly connected with the nodes in T such
that each node in T has a fixed indegree of N.
As multapses are per default allowed and possible with this rule, you can disallow them by adding 'allow_multapses': False to the conn_dict.
n, m, N = 5, 5, 2
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('iaf_psc_alpha', m)
conn_spec = {'rule': 'fixed_indegree', 'indegree': N}
nest.Connect(S, T, conn_spec)
Mathematical details: Random, fixed in-degree with multapses
The marginal distributions are binomial distributions
Mathematical details: Random, fixed in-degree without multapses
where \(\forall_j\,K_j\in\{0,1\}\). The marginal distributions are hypergeometric distributions
with \(\text{Ber}(p)\) denoting the Bernoulli distribution with parameter \(p\), because \(K\in\{0,1\}\). The full joint distribution is the sum of \(N_t\) independent instances of equation (1).
Random, fixed out-degree¶
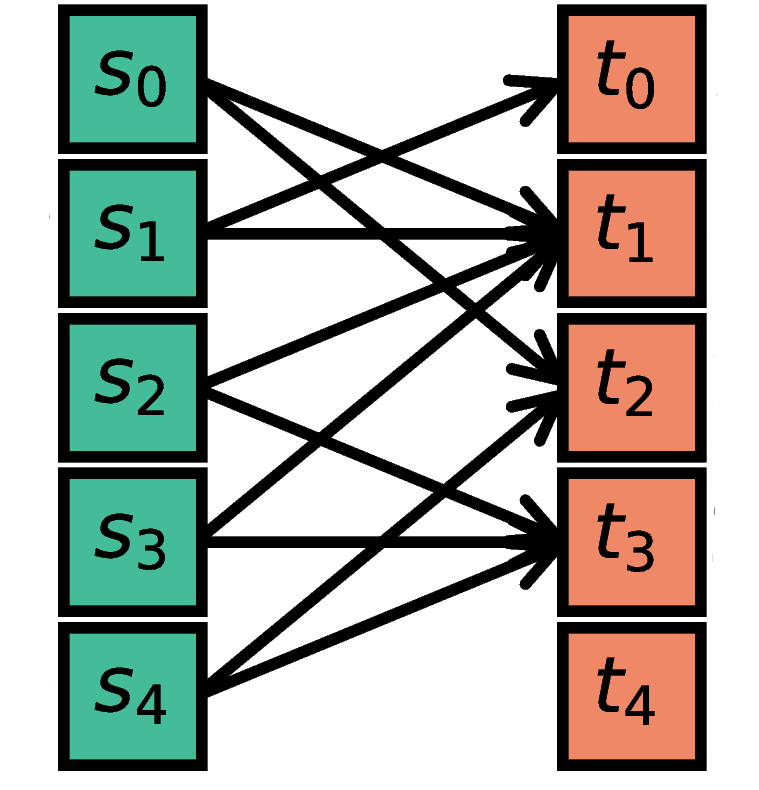
The nodes in S are randomly connected with the nodes in T such
that each node in S has a fixed outdegree of N.
As multapses are per default allowed and possible with this rule, you can disallow them by adding 'allow_multapses': False to the conn_dict.
n, m, N = 5, 5, 2
S = nest.Create('iaf_psc_alpha', n)
T = nest.Create('iaf_psc_alpha', m)
conn_spec = {'rule': 'fixed_outdegree', 'outdegree': N}
nest.Connect(S, T, conn_spec)
Mathematical details: Random, fixed out-degree with multapses
Mathematical details: Random, fixed out-degree without multapses
Tripartite Bernoulli with pool¶
For each possible pair of nodes from a source NodeCollection (e.g., a neuron population S)
and a target NodeCollection (e.g., a neuron population T), a connection is
created with probability p_primary, and these connections are
called ‘primary’ connections. For each primary connection, a
third-party connection pair involving a node from a third NodeCollection
(e.g., an astrocyte population A) is created with the conditional probability
p_third_if_primary. This connection pair includes a connection
from the S node to the A node, and a connection from the A node to the
T node. The A node to connect to is chosen
at random from a pool, a subset of the nodes in A. By default,
this pool is all of A.
Pool formation is controlled by parameters pool_type, which can be 'random'
(default) or 'block', and pool_size, which must be between 1
and the size of A (default). For random pools, for each node from
T, pool_size nodes from A are chosen randomly without
replacement.
For block pools, two variants exist. Let N_T and N_A be the number of
nodes in T and A, respectively. If pool_size == 1, the
first N_T/N_A nodes in T are assigned the first node in
A as their pool, the second N_T/N_A nodes in T the
second node in A and so forth. In this case, N_T must be a
multiple of N_A. If pool_size > 1, the first pool_size
elements of A are the pool for the first node in T, the
second pool_size elements of A are the pool for the second
node in T and so forth. In this case, N_T * pool_size == N_A
is required.
The following figure and code demonstrate three use case examples with
pool_type being 'random' or 'block':
(A) In the example of 'random' pool type, each node in T can be connected with
up to two randomly selected nodes in A (given pool_size == 2).
N_S, N_T, N_A, p_primary, p_third_if_primary = 6, 6, 3, 0.2, 1.0
pool_type, pool_size = 'random', 2
S = nest.Create('aeif_cond_alpha_astro', N_S)
T = nest.Create('aeif_cond_alpha_astro', N_T)
A = nest.Create('astrocyte_lr_1994', N_A)
conn_spec = {'rule': 'tripartite_bernoulli_with_pool',
'p_primary': p_primary,
'p_third_if_primary': p_third_if_primary,
'pool_type': pool_type,
'pool_size': pool_size}
syn_specs = {'third_out': 'sic_connection'}
nest.TripartiteConnect(S, T, A, conn_spec, syn_specs)
(B) In
the first example of 'block' pool type, let N_T/N_A = 2,
then each node in T can be connected with one node in A
(pool_size == 1 is required because N_A < N_T), and each node in
A can be connected with up to two nodes in T.
N_S, N_T, N_A, p_primary, p_third_if_primary = 6, 6, 3, 0.2, 1.0
pool_type, pool_size = 'block', 1
S = nest.Create('aeif_cond_alpha_astro', N_S)
T = nest.Create('aeif_cond_alpha_astro', N_T)
A = nest.Create('astrocyte_lr_1994', N_A)
conn_spec = {'rule': 'tripartite_bernoulli_with_pool',
'p_primary': p_primary,
'p_third_if_primary': p_third_if_primary,
'pool_type': pool_type,
'pool_size': pool_size}
syn_specs = {'third_out': 'sic_connection'}
nest.TripartiteConnect(S, T, A, conn_spec, syn_specs)
(C) In the second example
of 'block' pool type, let N_A/N_T = 2, then each node in
T can be connected with up to two nodes in A (pool_size == 2 is
required because N_A/N_T = 2), and each node in A can be
connected to one node in T.
N_S, N_T, N_A, p_primary, p_third_if_primary = 6, 3, 6, 0.2, 1.0
pool_type, pool_size = 'block', 2
S = nest.Create('aeif_cond_alpha_astro', N_S)
T = nest.Create('aeif_cond_alpha_astro', N_T)
A = nest.Create('astrocyte_lr_1994', N_A)
conn_spec = {'rule': 'tripartite_bernoulli_with_pool',
'p_primary': p_primary,
'p_third_if_primary': p_third_if_primary,
'pool_type': pool_type,
'pool_size': pool_size}
syn_specs = {'third_out': 'sic_connection'}
nest.TripartiteConnect(S, T, A, conn_spec, syn_specs)