NEST implementation of the aeif models¶
Hans Ekkehard Plesser and Tanguy Fardet, 2016-09-09¶
Updated by Hans Ekkehard Plesser, 2023-08-25¶
This notebook provides a reference solution for the Adaptive Exponential Integrate and Fire (AEIF) neuronal model and compares it with several numerical implementations using simpler solvers. In particular this justifies the change of implementation in September 2016 to make the simulation closer to the reference solution.
Position of the problem¶
Basics¶
The equations governing the evolution of the AEIF model are
when \(V < V_{peak}\) (threshold/spike detection). Once a spike occurs, we apply the reset conditions:
Divergence¶
In the AEIF model, the spike is generated by the exponential divergence. In practice, this means that just before threshold crossing (threshpassing), the argument of the exponential can become very large.
This can lead to numerical overflow or numerical instabilities in the solver, all the more if \(V_{peak}\) is large, or if \(\Delta_T\) is small.
Tested solutions¶
Old implementation (before September 2016)¶
The original solution was to bind the exponential argument to be smaller than 10 (ad hoc value to be close to the original implementation in BRIAN). As will be shown in the notebook, this solution does not converge to the reference LSODAR solution.
New implementation¶
The new implementation does not bind the argument of the exponential, but the potential itself, since according to the theoretical model, \(V\) should never get larger than \(V_{peak}\). We will show that this solution is not only closer to the reference solution in general, but also converges towards it as the timestep gets smaller.
Reference solution¶
The reference solution is implemented using the LSODAR solver which is described and compared in the following references:
Shampine LF, and Thompson S. (2000). Event location for ordinary differential equations. Computers and Mathematics with Applications, 39(5–6), 43–54. https://doi.org/10.1016/S0898-1221(00)00045-6
Thompson S (1987). A collection of test problems for ordinary differential equation solvers which have provisions for rootfinding (ORNL/TM-9912, 6111421; p. ORNL/TM-9912, 6111421). https://doi.org/10.2172/6111421
Dieci L, and Lopez L (2012). A survey of numerical methods for IVPs of ODEs with discontinuous right-hand side. Journal of Computational and Applied Mathematics, 236(16), 3967–3991. https://doi.org/10.1016/j.cam.2012.02.011
Hindmarsh, AC (1983). ODEPACK, a systematized collection of ODE solvers. In R. S. Stepleman & others (Eds.), Scientific computing (Vol. 1, pp. 55–64). North-Holland. https://computing.llnl.gov/sites/default/files/u88007.pdf
Petzold L. (1983). Automatic Selection of Methods for Solving Stiff and Nonstiff Systems of Ordinary Differential Equations. SIAM Journal on Scientific and Statistical Computing, 4(1), 136–148. https://doi.org/10.1137/0904010
Kahaner DK, Lawkins WF, and Thompson S. (1989). On the use of rootfinding ODE software for the solution of a common problem in nonlinear dynamical systems. Journal of Computational and Applied Mathematics, 28, 219–230. https://doi.org/10.1016/0377-0427(89)90334-8
Technical details and requirements¶
Implementation of the functions¶
The old and new implementations are reproduced using Scipy and are called by the
scipy_aeiffunctionThe NEST implementations are not shown here, but keep in mind that for a given time resolution, they are closer to the reference result than the scipy implementation since the GSL implementation uses a RK45 adaptive solver.
The reference solution using LSODAR, called
reference_aeif, is implemented through the assimulo package.
Requirements¶
To run this notebook, you need:
The assimulo package from PyPI is quite old and cannot be installed with current versions of Python distribution tools. If you use conda/mamba, you can install a current version of Assimulo from conda-forge. We have tested this notebook with assimulo 3.4.1.
[1]:
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"] = (15, 6)
Scipy functions mimicking the NEST code¶
Right hand side functions¶
[2]:
def rhs_aeif_new(y, _, p):
"""
New implementation bounding V < V_peak
Parameters
----------
y : list
Vector containing the state variables [V, w]
_ : unused var
p : Params instance
Object containing the neuronal parameters.
Returns
-------
dv : double
Derivative of V
dw : double
Derivative of w
"""
v = min(y[0], p.Vpeak)
w = y[1]
Ispike = 0.0
if p.DeltaT != 0.0:
Ispike = p.gL * p.DeltaT * np.exp((v - p.vT) / p.DeltaT)
dv = (-p.gL * (v - p.EL) + Ispike - w + p.Ie) / p.Cm
dw = (p.a * (v - p.EL) - w) / p.tau_w
return dv, dw
def rhs_aeif_old(y, _, p):
"""
Old implementation bounding the argument of the
exponential function (e_arg < 10.).
Parameters
----------
y : list
Vector containing the state variables [V, w]
_ : unused var
p : Params instance
Object containing the neuronal parameters.
Returns
-------
dv : double
Derivative of V
dw : double
Derivative of w
"""
v = y[0]
w = y[1]
Ispike = 0.0
if p.DeltaT != 0.0:
e_arg = min((v - p.vT) / p.DeltaT, 10.0)
Ispike = p.gL * p.DeltaT * np.exp(e_arg)
dv = (-p.gL * (v - p.EL) + Ispike - w + p.Ie) / p.Cm
dw = (p.a * (v - p.EL) - w) / p.tau_w
return dv, dw
Complete model¶
[3]:
def scipy_aeif(p, f, simtime, dt):
"""
Complete aeif model using scipy `odeint` solver.
Parameters
----------
p : Params instance
Object containing the neuronal parameters.
f : function
Right-hand side function (either `rhs_aeif_old`
or `rhs_aeif_new`)
simtime : double
Duration of the simulation (will run between
0 and tmax)
dt : double
Time increment.
Returns
-------
t : list
Times at which the neuronal state was evaluated.
y : list
State values associated to the times in `t`
s : list
Spike times.
vs : list
Values of `V` just before the spike.
ws : list
Values of `w` just before the spike
fos : list
List of dictionaries containing additional output
information from `odeint`
"""
t = np.arange(0, simtime, dt) # time axis
n = len(t)
y = np.zeros((n, 2)) # V, w
y[0, 0] = p.EL # Initial: (V_0, w_0) = (E_L, 5.)
y[0, 1] = 5.0 # Initial: (V_0, w_0) = (E_L, 5.)
s = [] # spike times
vs = [] # membrane potential at spike before reset
ws = [] # w at spike before step
fos = [] # full output dict from odeint()
# imitate NEST: update time-step by time-step
for k in range(1, n):
# solve ODE from t_k-1 to t_k
d, fo = odeint(f, y[k - 1, :], t[k - 1 : k + 1], (p,), full_output=True)
y[k, :] = d[1, :]
fos.append(fo)
# check for threshold crossing
if y[k, 0] >= p.Vpeak:
s.append(t[k])
vs.append(y[k, 0])
ws.append(y[k, 1])
y[k, 0] = p.Vreset # reset
y[k, 1] += p.b # step
return t, y, s, vs, ws, fos
LSODAR reference solution¶
Setting assimulo class¶
[4]:
from assimulo.solvers import LSODAR
from assimulo.problem import Explicit_Problem
class Extended_Problem(Explicit_Problem):
# need variables here for access
sw0 = [False]
ts_spikes = []
ws_spikes = []
Vs_spikes = []
def __init__(self, p):
self.p = p
self.y0 = [self.p.EL, 5.0] # V, w
# reset variables
self.ts_spikes = []
self.ws_spikes = []
self.Vs_spikes = []
# The right-hand-side function (rhs)
def rhs(self, t, y, sw):
"""
This is the function we are trying to simulate (aeif model).
"""
V, w = y[0], y[1]
Ispike = 0.0
if self.p.DeltaT != 0.0:
Ispike = self.p.gL * self.p.DeltaT * np.exp((V - self.p.vT) / self.p.DeltaT)
dotV = (-self.p.gL * (V - self.p.EL) + Ispike + self.p.Ie - w) / self.p.Cm
dotW = (self.p.a * (V - self.p.EL) - w) / self.p.tau_w
return np.array([dotV, dotW])
# Sets a name to our function
name = "AEIF_nosyn"
# The event function
def state_events(self, t, y, sw):
"""
This is our function that keeps track of our events. When the sign
of any of the events has changed, we have an event.
"""
event_0 = -5 if y[0] >= self.p.Vpeak else 5 # spike
if event_0 < 0:
if not self.ts_spikes:
self.ts_spikes.append(t)
self.Vs_spikes.append(y[0])
self.ws_spikes.append(y[1])
elif self.ts_spikes and not np.isclose(t, self.ts_spikes[-1], 0.01):
self.ts_spikes.append(t)
self.Vs_spikes.append(y[0])
self.ws_spikes.append(y[1])
return np.array([event_0])
# Responsible for handling the events.
def handle_event(self, solver, event_info):
"""
Event handling. This functions is called when Assimulo finds an event as
specified by the event functions.
"""
ev = event_info
event_info = event_info[0] # only look at the state events information.
if event_info[0] > 0:
solver.sw[0] = True
solver.y[0] = self.p.Vreset
solver.y[1] += self.p.b
else:
solver.sw[0] = False
def initialize(self, solver):
solver.h_sol = []
solver.nq_sol = []
def handle_result(self, solver, t, y):
Explicit_Problem.handle_result(self, solver, t, y)
# Extra output for algorithm analysis
if solver.report_continuously:
h, nq = solver.get_algorithm_data()
solver.h_sol.extend([h])
solver.nq_sol.extend([nq])
LSODAR reference model¶
[5]:
def reference_aeif(p, simtime):
"""
Reference aeif model using LSODAR.
Parameters
----------
p : Params instance
Object containing the neuronal parameters.
f : function
Right-hand side function (either `rhs_aeif_old`
or `rhs_aeif_new`)
simtime : double
Duration of the simulation (will run between
0 and tmax)
dt : double
Time increment.
Returns
-------
t : list
Times at which the neuronal state was evaluated.
y : list
State values associated to the times in `t`
s : list
Spike times.
vs : list
Values of `V` just before the spike.
ws : list
Values of `w` just before the spike
h : list
List of the minimal time increment at each step.
"""
# Create an instance of the problem
exp_mod = Extended_Problem(p) # Create the problem
exp_sim = LSODAR(exp_mod) # Create the solver
exp_sim.atol = 1.0e-8
exp_sim.report_continuously = True
exp_sim.store_event_points = True
exp_sim.verbosity = 30
# Simulate
t, y = exp_sim.simulate(simtime) # Simulate 10 seconds
return t, y, exp_mod.ts_spikes, exp_mod.Vs_spikes, exp_mod.ws_spikes, exp_sim.h_sol
Set the parameters and simulate the models¶
Params (chose a dictionary)¶
[6]:
# Regular spiking
aeif_param = {
"V_reset": -58.0,
"V_peak": 0.0,
"V_th": -50.0,
"I_e": 420.0,
"g_L": 11.0,
"tau_w": 300.0,
"E_L": -70.0,
"Delta_T": 2.0,
"a": 3.0,
"b": 0.0,
"C_m": 200.0,
"V_m": -70.0, #! must be equal to E_L
"w": 5.0, #! must be equal to 5.
"tau_syn_ex": 0.2,
}
# Bursting
aeif_param2 = {
"V_reset": -46.0,
"V_peak": 0.0,
"V_th": -50.0,
"I_e": 500.0,
"g_L": 10.0,
"tau_w": 120.0,
"E_L": -58.0,
"Delta_T": 2.0,
"a": 2.0,
"b": 100.0,
"C_m": 200.0,
"V_m": -58.0, #! must be equal to E_L
"w": 5.0, #! must be equal to 5.
}
# Close to chaos (use resolution < 0.005 and simtime = 200)
aeif_param3 = {
"V_reset": -48.0,
"V_peak": 0.0,
"V_th": -50.0,
"I_e": 160.0,
"g_L": 12.0,
"tau_w": 130.0,
"E_L": -60.0,
"Delta_T": 2.0,
"a": -11.0,
"b": 30.0,
"C_m": 100.0,
"V_m": -60.0, #! must be equal to E_L
"w": 5.0, #! must be equal to 5.
}
class Params:
"""
Class giving access to the neuronal
parameters.
"""
def __init__(self):
self.params = aeif_param
self.Vpeak = aeif_param["V_peak"]
self.Vreset = aeif_param["V_reset"]
self.gL = aeif_param["g_L"]
self.Cm = aeif_param["C_m"]
self.EL = aeif_param["E_L"]
self.DeltaT = aeif_param["Delta_T"]
self.tau_w = aeif_param["tau_w"]
self.a = aeif_param["a"]
self.b = aeif_param["b"]
self.vT = aeif_param["V_th"]
self.Ie = aeif_param["I_e"]
p = Params()
Simulate the 3 implementations¶
[7]:
# Parameters of the simulation
simtime = 100.0
resolution = 0.01
t_old, y_old, s_old, vs_old, ws_old, fo_old = scipy_aeif(p, rhs_aeif_old, simtime, resolution)
t_new, y_new, s_new, vs_new, ws_new, fo_new = scipy_aeif(p, rhs_aeif_new, simtime, resolution)
t_ref, y_ref, s_ref, vs_ref, ws_ref, h_ref = reference_aeif(p, simtime)
Final Run Statistics: AEIF_nosyn
Number of steps : 2013
Number of function evaluations : 5590
Number of Jacobian evaluations : 0
Number of state function evaluations : 2042
Number of state events : 7
Solver options:
Solver : LSODAR
Absolute tolerances : [1.e-08 1.e-08]
Relative tolerances : 1e-06
Starter : classical
Simulation interval : 0.0 - 100.0 seconds.
Elapsed simulation time: 0.06999148603063077 seconds.
/var/folders/5k/0gyqhsf50418tc1x1l1t5lsw0000gn/T/ipykernel_86976/3648738050.py:44: DeprecationWarning: The truth value of an empty array is ambiguous. Returning False, but in future this will result in an error. Use `array.size > 0` to check that an array is not empty.
t, y = exp_sim.simulate(simtime) # Simulate 10 seconds
Plot the results¶
Zoom out¶
[8]:
fig, ax = plt.subplots()
ax2 = ax.twinx()
# Plot the potentials
ax.plot(t_ref, y_ref[:, 0], linestyle="-", label="V ref.")
ax.plot(t_old, y_old[:, 0], linestyle="-.", label="V old")
ax.plot(t_new, y_new[:, 0], linestyle="--", label="V new")
# Plot the adaptation variables
ax2.plot(t_ref, y_ref[:, 1], linestyle="-", c="k", label="w ref.")
ax2.plot(t_old, y_old[:, 1], linestyle="-.", c="m", label="w old")
ax2.plot(t_new, y_new[:, 1], linestyle="--", c="y", label="w new")
# Show
ax.set_xlim([0.0, simtime])
ax.set_ylim([-65.0, 40.0])
ax.set_xlabel("Time (ms)")
ax.set_ylabel("V (mV)")
ax2.set_ylim([-20.0, 20.0])
ax2.set_ylabel("w (pA)")
ax.legend(loc=6)
ax2.legend(loc=2)
plt.show()
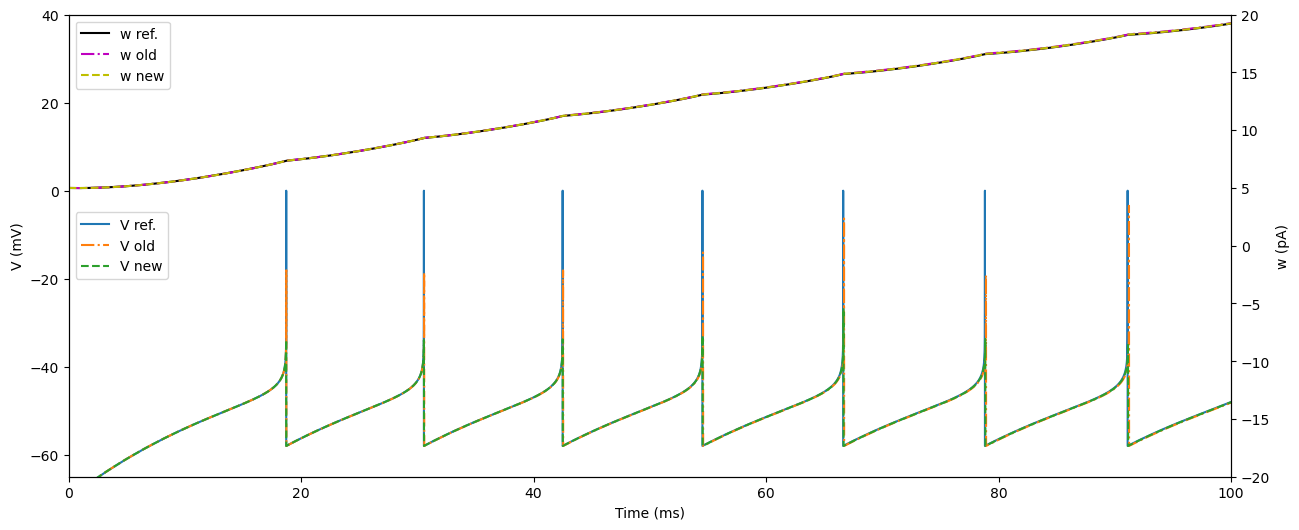
Zoom in¶
[9]:
fig, ax = plt.subplots()
ax2 = ax.twinx()
# Plot the potentials
ax.plot(t_ref, y_ref[:, 0], linestyle="-", label="V ref.")
ax.plot(t_old, y_old[:, 0], linestyle="-.", label="V old")
ax.plot(t_new, y_new[:, 0], linestyle="--", label="V new")
# Plot the adaptation variables
ax2.plot(t_ref, y_ref[:, 1], linestyle="-", c="k", label="w ref.")
ax2.plot(t_old, y_old[:, 1], linestyle="-.", c="y", label="w old")
ax2.plot(t_new, y_new[:, 1], linestyle="--", c="m", label="w new")
ax.set_xlim([90.0, 92.0])
ax.set_ylim([-65.0, 40.0])
ax.set_xlabel("Time (ms)")
ax.set_ylabel("V (mV)")
ax2.set_ylim([17.5, 18.5])
ax2.set_ylabel("w (pA)")
ax.legend(loc=5)
ax2.legend(loc=2)
plt.show()
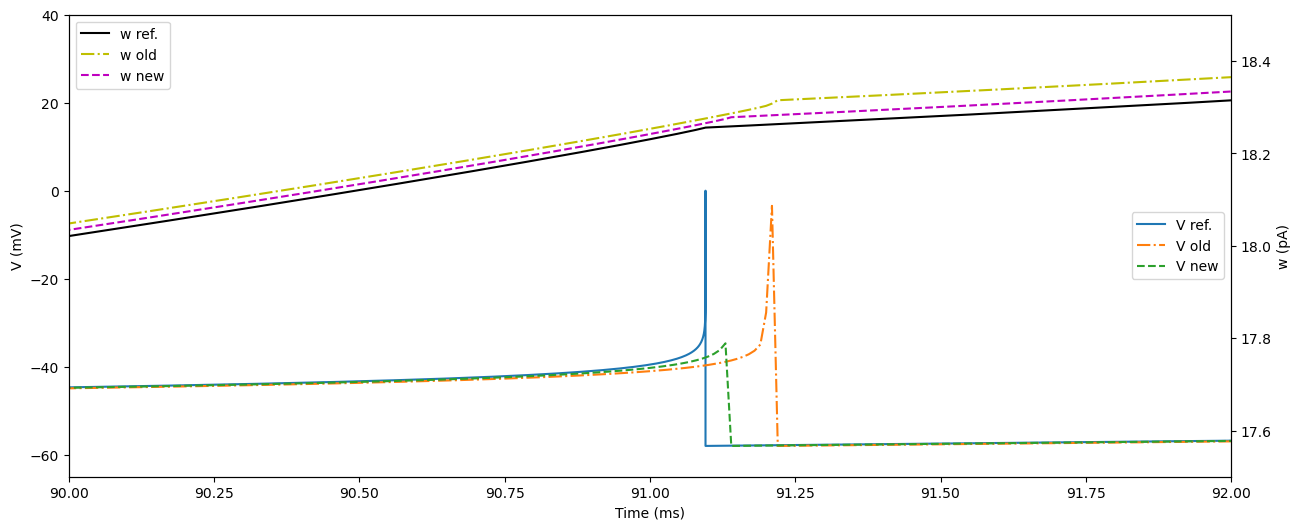
Compare properties at spike times¶
[10]:
print("spike times:\n-----------")
print("ref", np.around(s_ref, 3)) # ref lsodar
print("old", np.around(s_old, 3))
print("new", np.around(s_new, 3))
print("\nV at spike time:\n---------------")
print("ref", np.around(vs_ref, 3)) # ref lsodar
print("old", np.around(vs_old, 3))
print("new", np.around(vs_new, 3))
print("\nw at spike time:\n---------------")
print("ref", np.around(ws_ref, 3)) # ref lsodar
print("old", np.around(ws_old, 3))
print("new", np.around(ws_new, 3))
spike times:
-----------
ref [18.715 30.561 42.495 54.517 66.626 78.819 91.096]
old [18.73 30.59 42.54 54.58 66.71 78.92 91.22]
new [18.72 30.57 42.51 54.54 66.66 78.86 91.14]
V at spike time:
---------------
ref [0.006 0.03 0.025 0.036 0.033 0.031 0.041]
old [ 6.128 5.615 6.107 10.186 17.895 4.997 20.766]
new [32413643.009 32591616.326 35974587.74 51016349.64 77907589.627
37451353.635 11279320.152]
w at spike time:
---------------
ref [ 7.359 9.328 11.235 13.08 14.864 16.589 18.256]
old [ 7.367 9.344 11.258 13.111 14.906 16.637 18.315]
new [ 7.362 9.334 11.244 13.093 14.883 16.611 18.278]
Size of minimal integration timestep¶
[11]:
plt.semilogy(t_ref, h_ref, label="Reference")
plt.semilogy(t_old[1:], [d["hu"] for d in fo_old], linewidth=2, label="Old")
plt.semilogy(t_new[1:], [d["hu"] for d in fo_new], label="New")
plt.legend(loc=6)
plt.show();
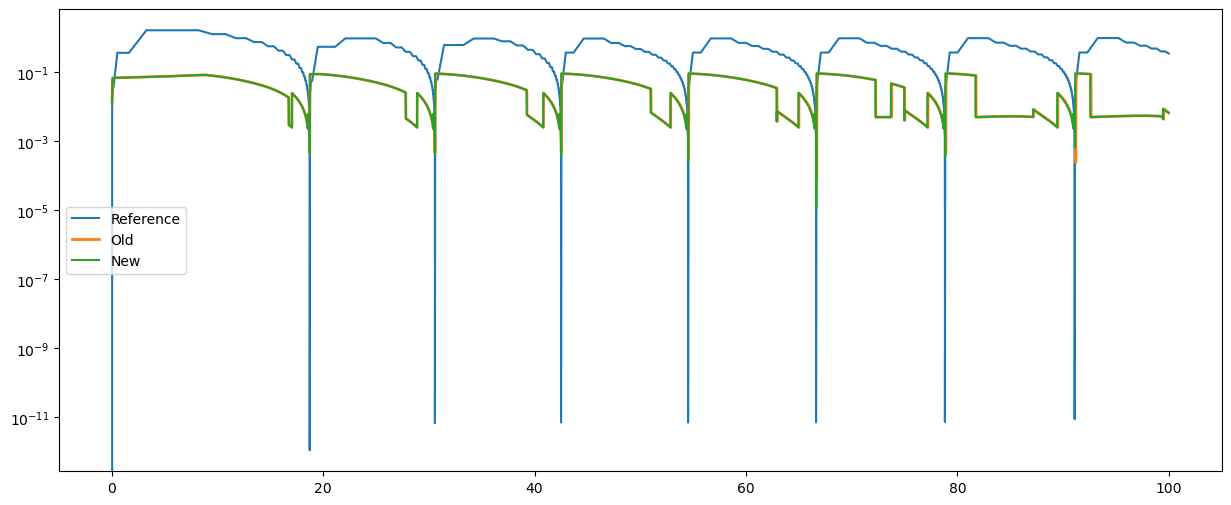
Convergence towards LSODAR reference with step size¶
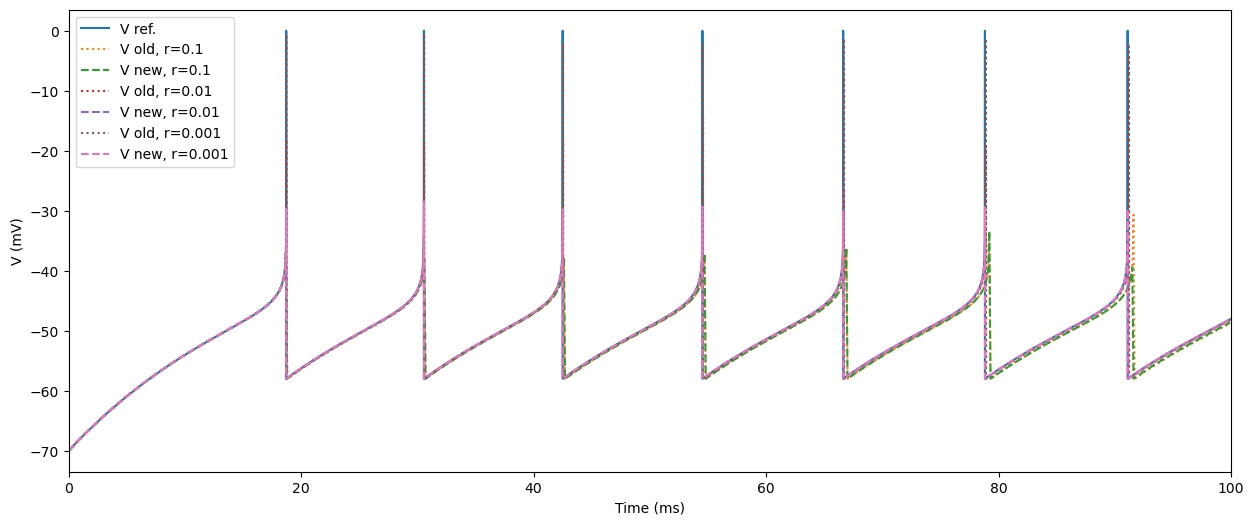
Zoom out¶
[12]:
plt.plot(t_ref, y_ref[:, 0], label="V ref.")
resolutions = (0.1, 0.01, 0.001)
di_res = {}
for resolution in resolutions:
t_old, y_old, _, _, _, _ = scipy_aeif(p, rhs_aeif_old, simtime, resolution)
t_new, y_new, _, _, _, _ = scipy_aeif(p, rhs_aeif_new, simtime, resolution)
di_res[resolution] = (t_old, y_old, t_new, y_new)
plt.plot(t_old, y_old[:, 0], linestyle=":", label="V old, r={}".format(resolution))
plt.plot(t_new, y_new[:, 0], linestyle="--", linewidth=1.5, label="V new, r={}".format(resolution))
plt.xlim(0.0, simtime)
plt.xlabel("Time (ms)")
plt.ylabel("V (mV)")
plt.legend(loc=2)
plt.show();
lsoda-- warning..internal t (=r1) and h (=r2) are such that in the machine, t + h = t on the next step
(h = step size). solver will continue anyway in above, r1 = 0.6691731905434D+02 r2 = 0.4368716407574D-14
lsoda-- warning..internal t (=r1) and h (=r2) are such that in the machine, t + h = t on the next step
(h = step size). solver will continue anyway in above, r1 = 0.6691731905434D+02 r2 = 0.4368716407574D-14
lsoda-- warning..internal t (=r1) and h (=r2) are such that in the machine, t + h = t on the next step
(h = step size). solver will continue anyway in above, r1 = 0.6691731905434D+02 r2 = 0.4368716407574D-14
lsoda-- warning..internal t (=r1) and h (=r2) are such that in the machine, t + h = t on the next step
(h = step size). solver will continue anyway in above, r1 = 0.6691731905434D+02 r2 = 0.4368716407574D-14
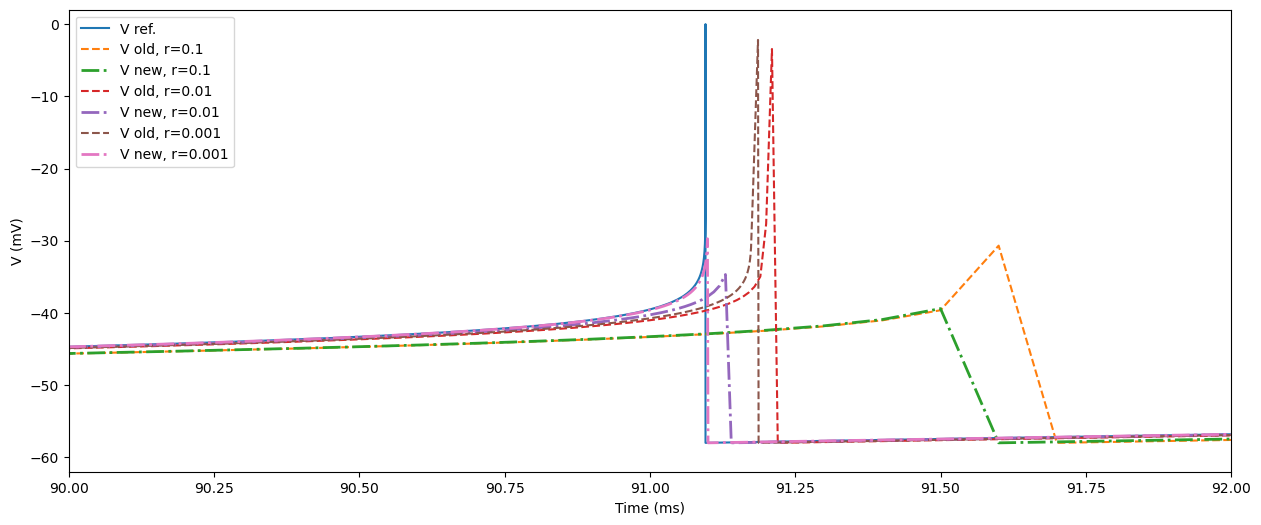
Zoom in¶
[13]:
plt.plot(t_ref, y_ref[:, 0], label="V ref.")
for resolution in resolutions:
t_old, y_old = di_res[resolution][:2]
t_new, y_new = di_res[resolution][2:]
plt.plot(t_old, y_old[:, 0], linestyle="--", label="V old, r={}".format(resolution))
plt.plot(t_new, y_new[:, 0], linestyle="-.", linewidth=2.0, label="V new, r={}".format(resolution))
plt.xlim(90.0, 92.0)
plt.ylim([-62.0, 2.0])
plt.xlabel("Time (ms)")
plt.ylabel("V (mV)")
plt.legend(loc=2)
plt.show();
License¶
This file is part of NEST. Copyright (C) 2004 The NEST Initiative
NEST is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 2 of the License, or (at your option) any later version.
NEST is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
