Spatially-structured networks¶
NEST provides a convenient interface for creating neurons placed in space and connecting those neurons with probabilities and properties depending on the relative placement of neurons. This permits the creation of complex networks with spatial structure.
This user manual provides an introduction to the functionalities provided for defining spatial networks in NEST. It is based exclusively on the PyNEST, the Python interface to NEST. NEST users using the SLI interface should be able to map instructions to corresponding SLI code. This manual is not meant as a comprehensive reference manual. Please consult the online documentation in PyNEST for details; where appropriate, that documentation also points to relevant SLI documentation.
This manual describes the spatial functionalities included with NEST 3.0.
In the next sections of this manual, we introduce the commands and concepts required to work with spatially distributed nodes. In particular,
section Connections describes how to connect spatial nodes with each other
section Inspecting spatially distributed NodeCollections explains how you can inspect and visualize spatial networks.
section Creating custom masks deals with creating connection boundaries using parameters, and the more advanced topic of extending the functionalities with custom masks provided by C++ classes in an extension module.
The Python scripts used throughout this manual are found in the NEST
sources under doc/htmldoc/networks/scripts.
There may be a number of undocumented features, which you may discover by browsing the code. These features are highly experimental and should not be used for simulations, as they have not been validated.
Spatially distributed nodes¶
Neuronal networks can have an organized spatial distribution, which we call layers. Layers are NodeCollections with spatial metadata. We will first illustrate how to place elements in simple grid-like layers, where each element is a single model neuron, before describing how the elements can be placed freely in space.
We will illustrate the definition and use of spatially distributed NodeCollections using examples.
NEST distinguishes between two classes of layers:
- grid-based layers
in which each element is placed at a location in a regular grid;
- free layers
in which elements can be placed arbitrarily in the plane.
Grid-based layers allow for more efficient connection-generation under certain circumstances.
Grid-based NodeCollections¶
A very simple example¶
We create a first, grid-based simple NodeCollection with the following command:
layer = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[5, 5]))
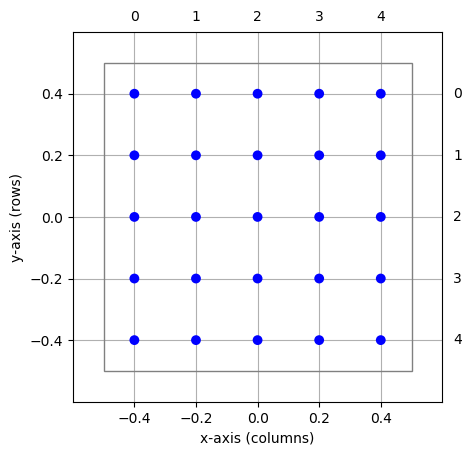
Figure 18 Simple grid-based NodeCollection centered about the origin. Blue circles mark the elements, the thin square the extent of the layer. Row and column indices are shown in the right and top margins, respectively.¶
The layer is shown in Figure 18. Note the following properties:
We are using the standard
Create()function, but in addition to model type, we are also passing anest.spatial.gridobject as thepositionsargument.The layer has five rows and five columns, as given by
shape=[columns, rows]. Note that a more intuitive way of thinking of shape is to think of it as given byshape=[num_x, num_y].The center of the NodeCollection is at the origin of the coordinate system, \((0,0)\).
The extent or size of the layer is \(1\times 1\). This is the default size for grid-based layers. The extent is marked by the thin square in Figure 18.
The grid spacing of the layer is
In the layer shown, we have \(dx=dy=0.2\), but the grid spacing may differ in x- and y-direction.
Layer elements are spaced by the grid spacing and are arranged symmetrically about the center.
The outermost elements are placed \(dx/2\) and \(dy/2\) from the borders of the extent.
Element positions in the coordinate system are given by \((x,y)\) pairs. The coordinate system follows that standard mathematical convention that the \(x\)-axis runs from left to right and the \(y\)-axis from bottom to top.
Each element of a grid-based NodeCollection has a row- and column-index in addition to its \((x,y)\)-coordinates. Indices are shown in the top and right margin of Figure 18. Note that row-indices follow matrix convention, i.e., run from top to bottom. Following pythonic conventions, indices run from 0.
Setting the extent¶
Grid-based layers have a default extent of \(1\times 1\). You can specify a
different extent of a layer, i.e., its size in \(x\)- and
\(y\)-direction by passing the extent argument to nest.spatial.grid():
layer = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[5, 5], extent=[2.0, 0.5]))
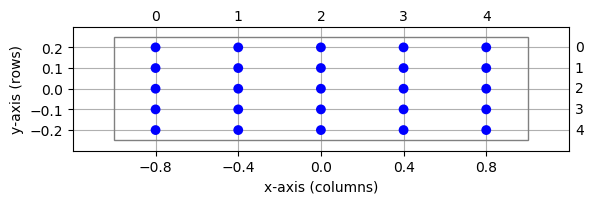
Figure 19 Same layer as in Figure 18, but with different extent.¶
The resulting NodeCollection is shown in Figure 19. The extent is always a two-element list of floats. In this example, we have grid spacings \(dx=0.4\) and \(dy=0.1\). Changing the extent does not affect grid indices.
The size of extent in \(x\)- and \(y\)-directions should
be numbers that can be expressed exactly as binary fractions. This is
automatically ensured for integer values. Otherwise, under rare
circumstances, subtle rounding errors may occur and trigger an
assertion, thus stopping NEST.
Setting the center¶
Layers are centered about the origin \((0,0)\) by default. This can
be changed by passing the center argument to nest.spatial.grid().
The following code creates layers centered about \((0,0)\),
\((-1,1)\), and \((1.5,0.5)\), respectively:
layer1 = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[5, 5]))
layer2 = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[5, 5], center=[-1.0, 1.0]))
layer3 = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[5, 5], center=[1.5, 0.5]))
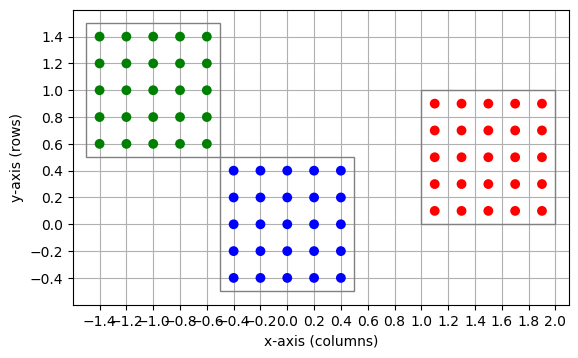
Figure 20 Three layers centered, respectively, about \((0,0)\) (blue), \((-1,-1)\) (green), and \((1.5,0.5)\) (red).¶
The center is given as a two-element list of floats. Changing the center does not affect grid indices: For each of the three layers in Figure 20, grid indices run from 0 to 4 through columns and rows, respectively, even though elements in these three layers have different positions in the global coordinate system.
The center coordinates should be numbers that can be expressed
exactly as binary fractions. For more information, see the section
Setting the extent.
Constructing a layer: an example¶
To see how to construct a layer, consider the following example:
a layer with \(n_y\) rows and \(n_x\) columns;
spacing between nodes is \(d\) in \(x\)- and \(y\)-directions;
the left edge of the extent shall be at \(x=0\);
the extent shall be centered about \(y=0\).
From Eq. (1), we see that the extent of the NodeCollection must be \((n_x d, n_y d)\). We now need to find the coordinates \((c_x, c_y)\) of the center of the layer. To place the left edge of the extent at \(x=0\), we must place the center of the layer at \(c_x=n_x d / 2\) along the \(x\)-axis, i.e., half the extent width to the right of \(x=0\). Since the layer is to be centered about \(y=0\), we have \(c_y=0\). Thus, the center coordinates are \((n_x d/2, 0)\). The layer is created with the following code and shown in Figure 21:
nx, ny = 5, 3
d = 0.1
layer = nest.Create(
"iaf_psc_alpha", positions=nest.spatial.grid(shape=[nx, ny], extent=[nx * d, ny * d], center=[nx * d / 2.0, 0.0])
)
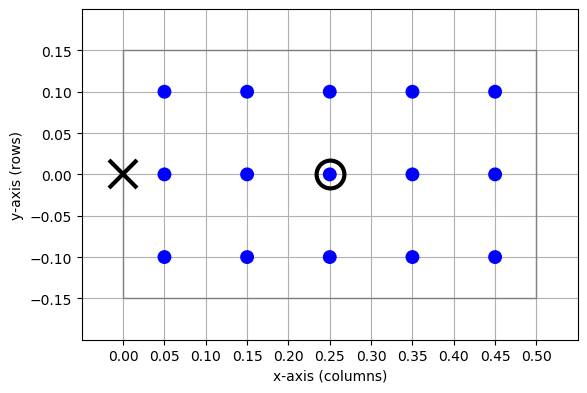
Figure 21 NodeCollection with \(n_x=5\) columns and \(n_y=3\) rows, spacing \(d=0.1\) and the left edge of the extent at \(x=0\), centered about the \(y\)-axis. The cross marks the point on the extent placed at the origin \((0,0)\), the circle the center of the layer.¶
Free layers¶
Free layers do not restrict node positions to a grid, but allow free
placement within the extent. To this end, the user can specify the
positions of all nodes explicitly, or pass a random distribution
parameter to nest.spatial.free(). The following code creates a NodeCollection of
50 iaf_psc_alpha neurons uniformly distributed in a layer with
extent \(1\times 1\), i.e., spanning the square
\([-0.5,0.5]\times[-0.5,0.5]\):
pos = nest.spatial.free(pos=nest.random.uniform(min=-0.5, max=0.5), num_dimensions=2)
layer = nest.Create("iaf_psc_alpha", 50, positions=pos)
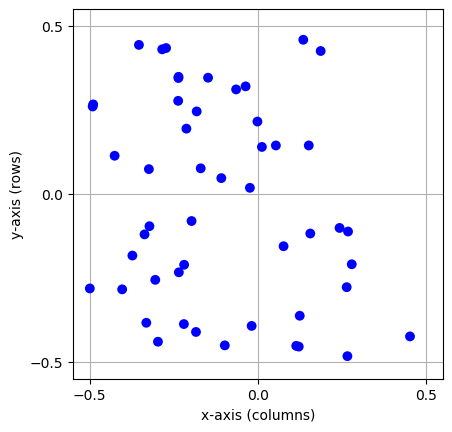
Figure 22 A free layer with 50 elements uniformly distributed in an extent of size \(1\times 1\).¶
Note the following points:
For free layers, element positions are specified by the
nest.spatial.freeobject.The
posentry must either be a Pythonlist(ortuple) of element coordinates, i.e., of two-element tuples of floats giving the (\(x\), \(y\))-coordinates of the elements, or aParameterobject.When using a parameter object for the positions, the number of dimensions have to be specified by the
num_dimensionsvariable. num_dimensions can either be 2 or 3.When using a parameter object you also need to specify how many elements you want to create by specifying
'n'in theCreate()call. This is not the case when you pass a list to thenest.spatial.freeobject.The extent is automatically set when using
nest.spatial.free, however, it is still possible to set the extent yourself by passing theextentvariable to the object.All element positions must be within the layer’s extent. Elements may be placed on the perimeter of the extent as long as no periodic boundary conditions are used; see the section Periodic boundary conditions.
To create a spatially distributed NodeCollection from a list, do the following:
pos = nest.spatial.free(pos=[[-0.5, -0.5], [-0.25, -0.25], [0.75, 0.75]])
layer = nest.Create("iaf_psc_alpha", positions=pos)
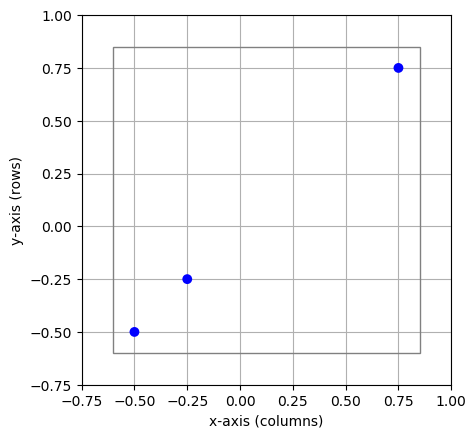
Figure 23 A free layer with 3 elements freely distributed space. The extent is given by the gray lines.¶
Note that when using a list to specify the positions, neither 'n' nor num_dimenstions
are specified. Furthermore, the extent is calculated from the node positions, and is here
\(1.45\times 1.45\). The extent could also be set by passing the extent argument.
3D layers¶
Although the term “layer” suggests a 2-dimensional structure, the layers in NEST may in fact be 3-dimensional. The example from the previous section may be easily extended by updating number of dimensions for the positions:
pos = nest.spatial.free(nest.random.uniform(min=-0.5, max=0.5), num_dimensions=3)
layer = nest.Create("iaf_psc_alpha", 200, positions=pos)
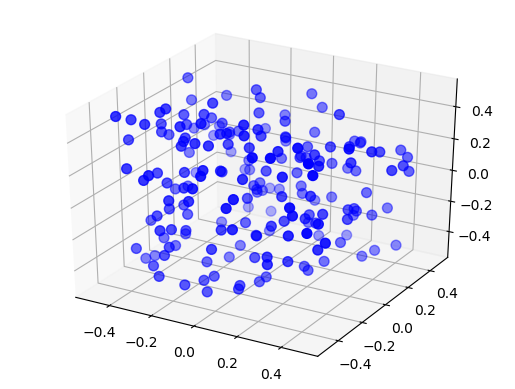
Figure 24 A free 3D layer with 200 elements uniformly distributed in an extent of size \(1\times 1\times 1\).¶
Again it is also possible to specify a list of list to create nodes in a 3-dimensional
space. Another possibility is to create a 3D grid-layer, with 3 elements passed to
the shape argument, shape=[nx, ny, nz]:
pos = nest.spatial.grid(shape=[4, 5, 6])
layer = nest.Create("iaf_psc_alpha", positions=pos)
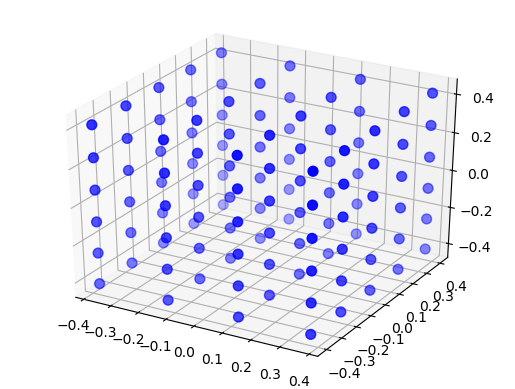
Figure 25 A grid 3D NodeCollection with 120 elements distributed on a grid with 4 elements in the x-direction, 5 elements in the y-direction and 6 elements in the z-direction, with an extent of size \(1\times 1\times 1\).¶
Periodic boundary conditions¶
Simulations usually model systems much smaller than the biological networks we want to study. One problem this entails is that a significant proportion of neurons in a model network is close to the edges of the network with fewer neighbors than nodes properly inside the network. In the \(5\times 5\)-layer in Figure 18 for instance., 16 out of 25 nodes form the border of the layer.
One common approach to reducing the effect of boundaries on simulations is to introduce periodic boundary conditions, so that the rightmost elements on a grid are considered nearest neighbors to the leftmost elements, and the topmost to the bottommost. The flat layer becomes the surface of a torus. Figure 26 illustrates this for a one-dimensional layer, which turns from a line to a ring upon introduction of periodic boundary conditions.
You specify periodic boundary conditions for a NodeCollection using
the entry edge_wrap:
layer = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[5, 1], extent=[5.0, 1.0], edge_wrap=True))
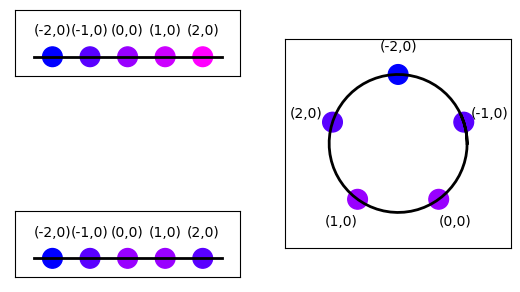
Figure 26 Top left: Layer with single row and five columns without periodic boundary conditions. Numbers above elements show element coordinates. Colors shifting from blue to magenta mark increasing distance from the element at \((-2,0)\). Bottom left: Same layer, but with periodic boundary conditions. Note that the element at \((2,0)\) now is a nearest neighbor to the element at \((-2,0)\). Right: Layer with periodic boundary condition arranged on a circle to illustrate neighborhood relationships.¶
Note that the longest possible distance between two elements in a layer without periodic boundary conditions is
but only
for a layer with periodic boundary conditions; \(x_{\text{ext}}\) and \(y_{\text{ext}}\) are the components of the extent size.
We will discuss the consequences of periodic boundary conditions more in the section on Connections.
Layers as NodeCollection¶
From the perspective of NEST, a layer is a special type of NodeCollection. From the user perspective, the following points may be of interest:
The NodeCollection has a
spatialproperty describing the spatial properties of the NodeCollection (lis the layer created at the beginning of this guide):
print(layer.spatial)
The spatial property is read-only; changing any value will
not change properties of the spatially distributed NodeCollection.
NEST sees the elements of the layer in the same way as the elements of any other NodeCollection. NodeCollections created as layers can therefore be used in the same ways as any standard NodeCollection. However, operations requiring a NodeCollection with spatial data (e.g.
Connect()with spatial dependence, or visualization of layers) can only be used on NodeCollections created with spatial distribution.
nest.PrintNodes()
Connections¶
The most important feature of the spatially-structured networks is the ability to
create connections between NodeCollections with quite some flexibility. In this
chapter, we will illustrate how to specify and create connections. All
connections are created using the Connect() function.
Basic principles¶
Terminology¶
We begin by introducing important terminology:
- Connection
In the context of connections between the elements of NodeCollections with spatial distributions, we often call the set of all connections between pairs of network nodes created by a single call to
Connect()a connection.- Connection dictionary
A dictionary specifying the properties of a connection between two NodeCollections in a call to
Connect().- Source
The source of a single connection is the node sending signals (usually spikes). In a projection, the source layer is the layer from which source nodes are chosen.
- Target
The target of a single connection is the node receiving signals (usually spikes). In a projection, the target layer is the layer from which target nodes are chosen.
- Driver
When connecting two layers, the driver layer is the one in which each node is considered in turn.
- Pool
- When connecting two layers, the pool layer is the one from which nodes are chosen for each node in the driver layer. I.e., we have
Connection parameters
Driver
Pool
rule='fixed_indegree'target layer
source layer
rule='fixed_outdegree'source layer
target layer
rule='pairwise_bernoulli'source layer
target layer
rule='pairwise_bernoulli'anduse_on_source=Truetarget layer
source layer
rule='pairwise_poisson'source layer
target layer
- Displacement
The displacement between a driver and a pool node is the shortest vector connecting the driver to the pool node, taking boundary conditions into account.
- Distance
The distance between a driver and a pool node is the length of their displacement.
- Mask
The mask defines which pool nodes are at all considered as potential targets for each driver node. See section Masks for details.
- Connection probability or
p The connection probability, specified as
pin the connection specifications, is either a value, or a parameter which specifies the probability for creating a connection between a driver and a pool node. The default probability is \(1\), i.e., connections are created with certainty. See section Probabilistic connection rules for details.- Pairwise average number of connections or
pairwise_avg_num_conns The pairwise average number of connections between a driver and a pool node. It is used in the
pairwise_poissonconnection rule and determines the mean value of the Poisson distribution from which the number of connections between the nodes is sampled. See section Probabilistic connection rules for details.- Autapse
An autapse is a synapse (connection) from a node onto itself. Autapses are permitted by default, but can be disabled by adding
'allow_autapses': Falseto the connection dictionary.- Multapse
Node A is connected to node B by a multapse if there are synapses (connections) from A to B. Multapses are permitted by default, but can be disabled by adding
'allow_multapses': Falseto the connection dictionary.
Connecting spatially distributed nodes¶
As with “normal” NodeCollections, connections between spatially distributed nodes are created
by calling Connect(). However, having spatial information about the nodes makes
position-based options available, and so in addition to the usual connection
schemes there exists additional connection parameters for spatially distributed
NodeCollections.
In many cases when connecting spatially distributed NodeCollections, a mask will be specified. Mask specifications are described in the section Masks. Only neurons within the mask are considered as potential sources or targets. If no mask is given, all neurons in the respective NodeCollection are considered sources or targets.
Here is a simple example, cf. Figure 27
spatial_nodes = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[11, 11], extent=[11.0, 11.0]))
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"rectangular": {"lower_left": [-2.0, -1.0], "upper_right": [2.0, 1.0]}},
}
nest.Connect(spatial_nodes, spatial_nodes, conndict)
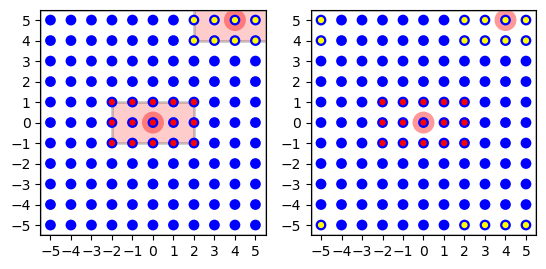
Figure 27 Left: Minimal connection example from a layer onto itself using a rectangular mask shown as red for the node at \((0,0)\) (marked light red). The targets of this node are marked with red dots. The targets for the node at \((4,5)\) are marked with yellow dots. This node has fewer targets since it is at the corner and many potential targets are beyond the layer. Right: The effect of periodic boundary conditions is seen here. Source and target layer and connection dictionary were identical, except that periodic boundary conditions were used. The node at \((4,5)\) now has 15 targets, too, but they are spread across the corners of the layer. If we wrapped the layer to a torus, they would form a \(5\times 3\) rectangle centered on the node at \((4,5)\).¶
In this example, layer l is both source and target layer. For each
node in the NodeCollection we choose targets according to the rectangular mask
centered about each source node. Since the connection probability is 1.0,
we connect to all nodes within the mask. Note the effect of normal and
periodic boundary conditions on the connections created for different
nodes in the NodeCollection, as illustrated in Figure 27.
Mapping source and target layers¶
The application of masks and other functions depending on the distance or even the displacement between nodes in the source and target layers requires a mapping of coordinate systems between source and target layers. NEST applies the following coordinate mapping rules:
All layers have two-dimensional Euclidean coordinate systems.
No scaling or coordinate transformation can be applied between NodeCollections with spatial distribution.
The displacement \(d(D,P)\) from node \(D\) in the driver layer to node \(P\) in the pool layer is measured by first mapping the position of \(D\) in the driver layer to the identical position in the pool layer and then computing the displacement from that position to \(P\). If the pool layer has periodic boundary conditions, they are taken into account. It does not matter for displacement computations whether the driver layer has periodic boundary conditions.
Masks¶
A mask describes which area of the pool layer shall be searched for nodes when connecting for any given node in the driver layer. We will first describe geometrical masks defined for all layer types and then consider grid-based masks for grid-based NodeCollections. If no mask is specified, all nodes in the pool layer will be searched.
Note that the mask size should not exceed the size of the layer when using periodic boundary conditions, since the mask would “wrap around” in that case and pool nodes would be considered multiple times as targets.
If none of the mask types provided in the library meet your need, you may define custom masks, either by introducing a cut-off to the connection probability using parameters, or by adding more mask types in a NEST extension module. This is covered in the section on Creating custom masks.
Masks for 2D layers¶
NEST currently provides four types of masks usable for 2-dimensional free and grid-based NodeCollections. They are illustrated in Figure 28. The masks are
- Rectangular
All nodes within a rectangular area are connected. The area is specified by its lower left and upper right corners, measured in the same unit as element coordinates. Example:
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"rectangular": {"lower_left": [-2.0, -1.0], "upper_right": [2.0, 1.0]}},
}
- Circular
All nodes within a circle are connected. The area is specified by its radius.
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"circular": {"radius": 2.0}}}
- Doughnut
All nodes between an inner and outer circle are connected. Note that nodes on the inner circle are not connected. The area is specified by the radii of the inner and outer circles.
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"doughnut": {"inner_radius": 1.5, "outer_radius": 3.0}}}
- Elliptical
All nodes within an ellipsis are connected. The area is specified by its major and minor axis.
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"elliptical": {"major_axis": 7.0, "minor_axis": 4.0}}}
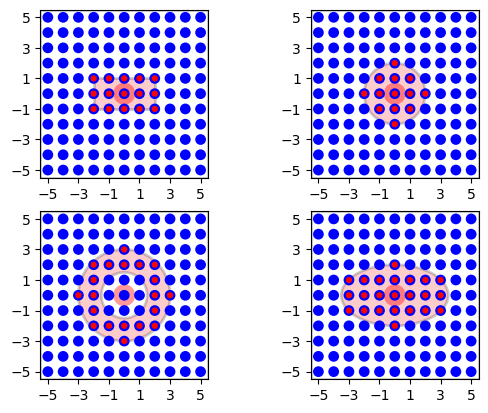
Figure 28 Masks for 2D layers. For all mask types, the driver node is marked by a wide light-red circle, the selected pool nodes by red dots and the masks are red. From left to right, top to bottom: rectangular, circular, doughnut and elliptical masks centered about the driver node.¶
By default, the masks are centered about the position of the driver
node, mapped into the pool layer. You can change the location of the
mask relative to the driver node by specifying an 'anchor' entry in
the mask dictionary. The anchor is a 2D vector specifying the location
of the mask center relative to the driver node, as in the following
examples (cf. Figure 29).
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"rectangular": {"lower_left": [-2.0, -1.0], "upper_right": [2.0, 1.0]}, "anchor": [-1.5, -1.5]},
}
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"circular": {"radius": 2.0}, "anchor": [-2.0, 0.0]}}
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"doughnut": {"inner_radius": 1.5, "outer_radius": 3.0}, "anchor": [1.5, 1.5]},
}
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"elliptical": {"major_axis": 7.0, "minor_axis": 4.0}, "anchor": [2.0, -1.0]},
}
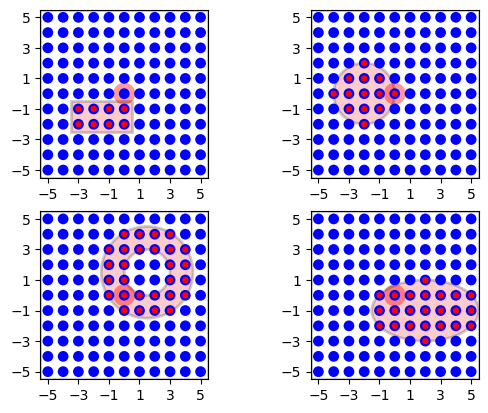
Figure 29 The same masks as in Figure 28, but centered about
\((-1.5,-1.5)\), \((-2,0)\), \((1.5,1.5)\) and
\((2, -1)\), respectively, using the 'anchor' parameter.¶
It is, as of NEST 2.16, possible to rotate the \(\textbf{rectangular}\)
and \(\textbf{elliptical}\) masks, see Fig Figure 29. To do so,
add an 'azimuth_angle' entry in the specific mask dictionary. The
azimuth_angle is measured in degrees and is the rotational angle
from the x-axis to the y-axis.
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"rectangular": {"lower_left": [-2.0, -1.0], "upper_right": [2.0, 1.0], "azimuth_angle": 120.0}},
}
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"elliptical": {"major_axis": 7.0, "minor_axis": 4.0, "azimuth_angle": 45.0}},
}
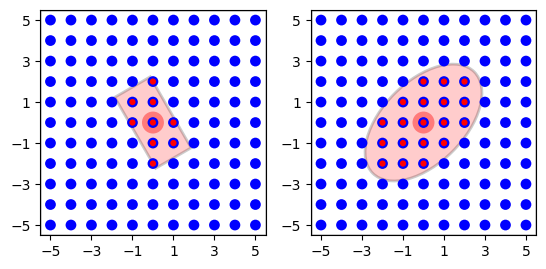
Figure 30 Rotated rectangular and elliptical mask from Figure 28 and Figure 29, where the rectangular mask is rotated \(120^\circ\) and the elliptical mask is rotated \(45^\circ\).¶
Masks for 3D layers¶
Similarly, there are three mask types that can be used for 3D NodeCollections,
- Box
All nodes within a cuboid volume are connected. The area is specified by its lower left and upper right corners, measured in the same unit as element coordinates. Example:
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"box": {"lower_left": [-2.0, -1.0, -1.0], "upper_right": [2.0, 1.0, 1.0]}},
}
- Spherical
All nodes within a sphere are connected. The area is specified by its radius.
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"spherical": {"radius": 2.5}}}
- Ellipsoidal
All nodes within an ellipsoid are connected. The area is specified by its major, minor, and polar axis.
conndict = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"ellipsoidal": {"major_axis": 7.0, "minor_axis": 4.0, "polar_axis": 4.5}},
}
As in the 2D case, you can change the location of the mask relative to
the driver node by specifying a 3D vector in the 'anchor' entry in
the mask dictionary. If you want to rotate the box or ellipsoidal masks,
you can add an 'azimuth_angle' entry in the specific mask dictionary
for rotation from the x-axis towards the y-axis about the z-axis, or a
'polar_angle' entry, specifying the rotation angle in degrees from
the z-axis about the (possibly rotated) x axis, from the (possibly
rotated) y-axis. You can specify both at once of course. If both are
specified, we first rotate about the z-axis and then about the new
x-axis. NEST currently does not support rotation in all three directions,
the rotation from the y-axis about the (possibly rotated) z-axis, from
the (possibly rotated) x-axis is missing.
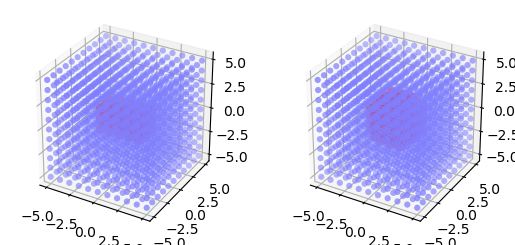
Figure 31 Masks for 3D NodeCollections. For all mask types, the driver node is marked by a wide light-red circle, the selected pool nodes by red dots and the masks are red. From left to right: box and spherical masks centered about the driver node.¶
Masks for grid-based layers¶
Grid-based layers can be connected using rectangular grid masks. For these, you specify the size of the mask not by lower left and upper right corner coordinates, but give their size in x and y direction, as in this example:
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"grid": {"shape": [5, 3]}}}
The resulting connections are shown in Figure 32. By default the top-left corner of a grid mask, i.e., the grid mask element with grid index \([0,0]\)(see 2.1.1), is aligned with the driver node. You can change this alignment by specifying an anchor for the mask:
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"grid": {"shape": [5, 3]}, "anchor": [2, 1]}}
You can even place the anchor outside the mask:
conndict = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"grid": {"shape": [3, 5]}, "anchor": [2, -1]}}
The resulting connection patterns are shown in Figure 32.
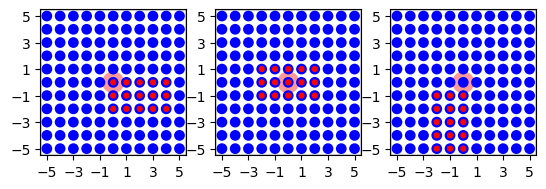
Figure 32 Grid masks for connections between grid-based layers. Left: \(5\times 3\) mask with default alignment at upper left corner. Center: Same mask, but anchored to center node at grid index \([1,2]\). Right: Same mask, but anchor to the upper left of the mask at grid index \([-1,2]\).¶
Connections specified using grid masks are generated more efficiently than connections specified using other mask types.
Note the following:
Grid-based masks are applied by considering grid indices. The position of nodes in physical coordinates is ignored.
In consequence, grid-based masks should only be used between NodeCollections with identical grid spacings.
The semantics of the
'anchor'property for grid-based masks differ significantly for general masks described in the section Masks for 2D layers. For general masks, the anchor is the center of the mask relative to the driver node. For grid-based nodes, the anchor determines which mask element is aligned with the driver element.
Probabilistic connection rules¶
Many neuronal network models employ probabilistic connection rules.
NEST supports probabilistic connections through the
pairwise_bernoulli and the pairwise_poisson connection rule.
For the pairwise_bernoulli rule, the probability can then be a
constant, depend on the position of the source or the target neuron,
or on the distance between a driver and a pool node to a connection probability.
For the pairwise_poisson rule, the pairwise average number of connections
can depend on the position of the source or the target neuron,
or on the distance between a driver and a pool node to a connection probability.
To create dependencies on neuron positions, NEST Parameter objects are used.
NEST then generates a connection according to this probability.
Probabilistic connections between layers can be generated in two different ways:
- Free probabilistic connections using
pairwise_bernoulli In this case,
Connect()considers each driver node \(D\) in turn. For each \(D\), it evaluates the parameter value for each pool node \(P\) within the mask and creates a connection according to the resulting probability. This means in particular that each possible driver-pool pair is inspected exactly once and that there will be at most one connection between each driver-pool pair.- Free probabilistic connections using
pairwise_poisson In this case,
Connect()considers each driver node \(D\) in turn. For each \(D\), it evaluates the parameter value for each pool node \(P\) within the mask and creates a number of connections that are sampled from a Poisson distribution with mean of the parameter value. This means in particular that each possible driver-pool pair is inspected exactly once and that more than one connection between each driver-pool pair is possible. Additionally, the parameter may be larger than \(1\).- Prescribed number of connections
can be obtained by using
fixed_indegreeorfixed_outdegreeconnection rule, and specifying the number of connections to create per driver node. See the section Prescribed number of connections for details.
A selection of specific NEST parameters pertaining to spatially structured networks are shown the table below.
NEST parameters specific to spatially-structured networks¶
The parameters in the table below represent positions of neurons or distances between two neurons. To set node parameters, only the node position can be used. The others can only be used when connecting.
Parameter
Description
nest.spatial.pos.xnest.spatial.pos.ynest.spatial.pos.znest.spatial.source_pos.xnest.spatial.source_pos.ynest.spatial.source_pos.znest.spatial.target_pos.xnest.spatial.target_pos.ynest.spatial.target_pos.znest.spatial.distancenest.spatial.distance.xnest.spatial.distance.ynest.spatial.distance.z
NEST provides some functions to help create distributions based on the position of the nodes, for instance the distance between two neurons, shown in the table below. The table also includes parameters drawing values from random distributions.
Distribution function
Arguments
Function
nest.spatial_distributions.exponential()
nest.spatial_distributions.gaussian()
nest.spatial_distributions.gaussian2D()
nest.spatial_distributions.gabor()
nest.spatial_distributions.gamma()
nest.random.uniform()\(p\in [\text{min},\text{max})\) uniformly
nest.random.normal()normal with given mean and standard deviation
nest.random.exponential()exponential with a given scale, \(\beta\)
nest.random.lognormal()lognormal with given mean and standard deviation, std
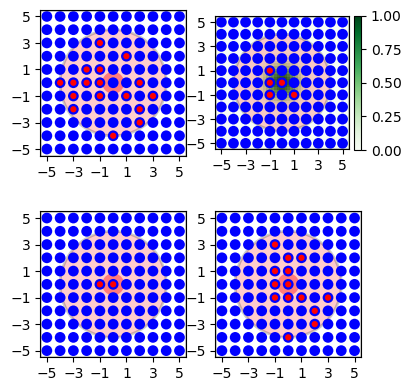
Figure 33 Illustration of various connection probabilities. Top left: constant probability, \(p=0.5\). Top right: Distance dependent Gaussian probability, green distribution show \(\sigma\). Bottom left: Same distance dependent Gaussian probability, but all \(p<0.5\) treated as \(p=0\). Bottom right: 2D-Gaussian.¶
Several examples follow. They are illustrated in Figure 33.
- Constant
Fixed connection probability:
conndict = {"rule": "pairwise_bernoulli", "p": 0.5, "mask": {"circular": {"radius": 4.0}}}
- Gaussian
The connection probability is a Gaussian distribution based on the distance between neurons. In the example, connection probability is 1 for \(d=0\) and falls off with a “standard deviation” of \(\sigma=1\):
conndict = {
"rule": "pairwise_bernoulli",
"p": nest.spatial_distributions.gaussian(nest.spatial.distance, std=1.0),
"mask": {"circular": {"radius": 4.0}},
}
- Cut-off Gaussian
In this example we have a distance-dependent Gaussian distributon, where all probabilities less than \(0.5\) are set to zero:
distribution = nest.spatial_distributions.gaussian(nest.spatial.distance, std=1.0)
conndict = {
"rule": "pairwise_bernoulli",
"p": nest.logic.conditional(distribution > 0.5, distribution, 0),
"mask": {"circular": {"radius": 4.0}},
}
- 2D Gaussian
Here we use a two-dimensional Gaussian distribution, i.e., a Gaussian with different widths in \(x\)- and \(y\)- directions. This probability depends on displacement, not only on distance:
conndict = {
"rule": "pairwise_bernoulli",
"p": nest.spatial_distributions.gaussian2D(nest.spatial.distance.x, nest.spatial.distance.y, std_x=1.0, std_y=3.0),
"mask": {"circular": {"radius": 4.0}},
}
- Rectified Gabor Function
We conclude with an example of a rectified Gabor distribution, i.e., a two-dimensional Gaussian distribution modulated with a spatial oscillation perpendicular to \(\theta\). This probability depends on the displacement along the coordinates axes, not the distance:
conndict = {
"rule": "pairwise_bernoulli",
"p": nest.spatial_distributions.gabor(
nest.spatial.target_pos.x - nest.spatial.source_pos.x,
nest.spatial.target_pos.y - nest.spatial.source_pos.y,
theta=np.pi / 4,
gamma=0.7,
),
}
Note that for pool layers with periodic boundary conditions, NEST
always uses the shortest possible displacement vector from driver to
pool neuron as nest.spatial.distance.
Weights and delays¶
Parameters, such as those presented in Table NEST parameters specific to spatially-structured networks, can
also be used to specify distance-dependent or randomized weights and
delays for the connections created by Connect(). Weight and delays are in NEST
passed along in a synapse dictionary to the Connect() call.
nest.Connect(nodes, nodes, conn_dict, syn_dict)
Figure Figure 34 illustrates weights and delays generated using these parameters. The code examples used to generate the figures are shown below. All examples use a spatially distributed NodeCollection of 51 nodes placed on a line; the line is centered about \((25,0)\), so that the leftmost node has coordinates \((0,0)\). The distance between neighboring elements is 1. The mask is rectangular, spans the entire NodeCollection and is centered about the driver node.
- Linear example
pos = nest.spatial.grid(shape=[51, 1], extent=[51.0, 1.0], center=[25.0, 0.0]) spatial_nodes = nest.Create("iaf_psc_alpha", positions=pos) cdict = { "rule": "pairwise_bernoulli", "p": 1.0, "mask": {"rectangular": {"lower_left": [-25.5, -0.5], "upper_right": [25.5, 0.5]}}, } sdict = {"weight": nest.math.max(1.0 - 0.05 * nest.spatial.distance, 0.0), "delay": 0.1 + 0.02 * nest.spatial.distance} nest.Connect(spatial_nodes, spatial_nodes, cdict, sdict)
Results are shown in the top panel of Figure 34. Connection weights and delays are shown for the leftmost neuron as driver. Weights drop linearly from \(1\). From the node at \((20,0)\) on, the cutoff sets weights to 0. There are no connections to nodes beyond \((25,0)\), since the mask extends only 25 units to the right of the driver. Delays increase in a stepwise linear fashion, as NEST requires delays to be multiples of the simulation resolution.
- Linear example with periodic boundary conditions
cdict = { "rule": "pairwise_bernoulli", "p": 1.0, "mask": {"rectangular": {"lower_left": [-25.5, -0.5], "upper_right": [25.5, 0.5]}}, } sdict = {"weight": nest.math.max(1.0 - 0.05 * nest.spatial.distance, 0.0), "delay": 0.1 + 0.02 * nest.spatial.distance}
Results are shown in the middle panel of Figure 34. This example is identical to the previous, except that the (pool) layer has periodic boundary conditions. Therefore, the left half of the mask about the node at \((0,0)\) wraps back to the right half of the layer and that node connects to all nodes in the layer.
- Various spatially dependent distributions
cdict = { "rule": "pairwise_bernoulli", "p": 1.0, "mask": {"rectangular": {"lower_left": [-25.5, -0.5], "upper_right": [25.5, 0.5]}}, } sdict = {"weight": nest.spatial_distributions.exponential(nest.spatial.distance, beta=5.0)}
cdict = { "rule": "pairwise_bernoulli", "p": 1.0, "mask": {"rectangular": {"lower_left": [-25.5, -0.5], "upper_right": [25.5, 0.5]}}, } sdict = {"weight": nest.spatial_distributions.gaussian(nest.spatial.distance, std=5.0)}
Results are shown in the bottom panel of Figure 34. It shows linear, exponential and Gaussian distributions of the distance between connected nodes, used with weight functions for the node at \((25,0)\).
- Randomized weights and delays
cdict = { "rule": "pairwise_bernoulli", "p": 1.0, "mask": {"rectangular": {"lower_left": [-25.5, -0.5], "upper_right": [25.5, 0.5]}}, } sdict = {"weight": nest.random.uniform(min=0.2, max=0.8)}
By using the
nest.random.uniform()parameter for weights or delays, one can obtain randomized values for weights and delays, as shown by the red circles in the bottom panel of Figure 34.
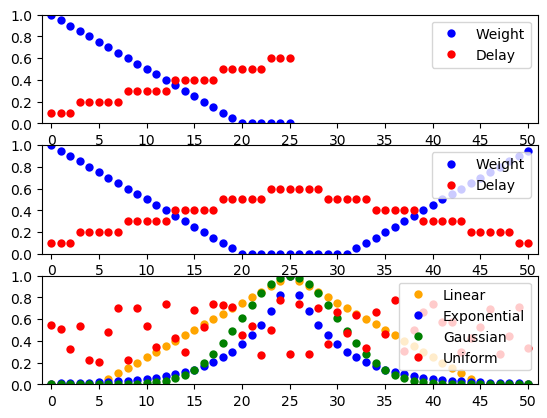
Figure 34 Distance-dependent and randomized weights and delays. See text for details.¶
Designing distance-dependent parameters¶
Although NEST comes with some pre-defined functions that can be used to create distributions of distance-dependent parameters, there is no limit to how parameters can be combined.
As an example, we will now combine some parameters to create a new parameter that is linear (actually affine) with respect to the displacement between the nodes, of the form
where \(d_x\) and \(d_y\) are the displacements between the source and target neuron on the x and y axis, respectively. The parameter is then simply:
parameter = 0.5 + nest.spatial.distance.x + 2.0 * nest.spatial.distance.y
This can be directly plugged into the Connect() function:
spatial_nodes = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[11, 11], extent=[1.0, 1.0]))
nest.Connect(
spatial_nodes, spatial_nodes, {"rule": "pairwise_bernoulli", "p": parameter, "mask": {"circular": {"radius": 0.5}}}
)
Periodic boundary conditions¶
Connections between layers with periodic boundary conditions are based on the following principles:
Periodic boundary conditions are always applied in the pool layer. It is irrelevant whether the driver layer has periodic boundary conditions or not.
By default, NEST does not accept masks that are wider than the pool layer when using periodic boundary conditions. Otherwise, one pool node could appear as multiple targets to the same driver node as the masks wraps several times around the layer. For layers with different extents in \(x\)- and \(y\)-directions this means that the maximum layer size is determined by the smaller extension.
nest.spatial.distanceand its single dimension variants always consider the shortest distance (displacement) between driver and pool node.
In most physical systems simulated using periodic boundary conditions, interactions between entities are short-range. Periodic boundary conditions are well-defined in such cases. In neuronal network models with long-range interactions, periodic boundary conditions may not make sense. In general, we recommend to use periodic boundary conditions only when connection masks are significantly smaller than the NodeCollections they are applied to.
Prescribed number of connections¶
We have so far described how to connect spatially distributed NodeCollections by either connecting to all nodes inside the mask or by considering each pool node in turn and connecting it according to a given probability function. In both cases, the number of connections generated depends on mask and connection probability.
Many neuron models in the literature, in contrast, prescribe a certain
fan in (number of incoming connections) or fan out (number of outgoing
connections) for each node. You can achieve this in NEST by
prescribing the number of connections for each driver node by using
fixed_indegree or fixed_outdegree as connection rule.
Connection generation now proceeds in a different way than before:
For each driver node,
Connect()randomly selects a node from the mask region in the pool layer, and creates a connection with the probability prescribed. This is repeated until the requested number of connections has been created.Thus, if all nodes in the mask shall be connected with equal probability, you should not specify a connection probability.
If you specify a probability with a distance-dependent distribution (e.g., Gaussian, linear, exponential), the connections will be distributed within the mask with the spatial profile given by the probability.
If you prohibit multapses (see section Terminology) and prescribe a number of connections greater than the number of pool nodes in the mask,
Connect()may get stuck in an infinite loop and NEST will hang. Keep in mind that the number of nodes within the mask may vary considerably for free layers with randomly placed nodes.If you use the connection rule
'rule': fixed_indegreein the connection dictionary, you also have to specify'indegree', the number of connections per target node.Similarly, if you use the connection rule
'rule': fixed_outdegreein the connection dictionary, you have to use'outdegree'to specify the number of connections per source node.
The following code generates a network of 1000 randomly placed nodes and connects them with a fixed fan out, of 50 outgoing connections per node distributed with a profile linearly decaying from unit probability to zero probability at distance \(0.5\). Multiple connections (multapses) between pairs of nodes are allowed, self-connections (autapses) prohibited. The probability of finding a connection at a certain distance is then given by the product of the probabilities for finding nodes at a certain distance with the probability value for this distance. For the connection probability and parameter values below we have
- The resulting distribution of distances between connected nodes is shown in
pos = nest.spatial.free(nest.random.uniform(-1.0, 1.0), extent=[2.0, 2.0], edge_wrap=True)
spatial_nodes = nest.Create("iaf_psc_alpha", 1000, positions=pos)
cdict = {
"rule": "fixed_outdegree",
"p": nest.math.max(1.0 - 2 * nest.spatial.distance, 0.0),
"mask": {"circular": {"radius": 1.0}},
"outdegree": 50,
"allow_multapses": True,
"allow_autapses": False,
}
nest.Connect(spatial_nodes, spatial_nodes, cdict)
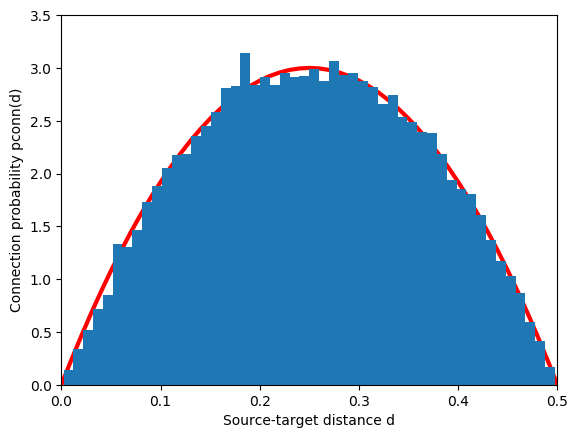
Figure 35 Distribution of distances between source and target for a network of 1000 randomly placed nodes, a fixed fan out of 50 connections and a connection probability decaying linearly from 1 to 0 at \(d=0.5\). The red line is the expected distribution from Eq. (2).¶
Functions determining weight and delay as function of distance/displacement work in just the same way as before when the number of connections is prescribed.
It is also possible to use a random parameter or spatially dependent parameter to set the number of incoming or outgoing connections.
cdict_random_in = {
"rule": "fixed_indegree",
"p": nest.spatial_distributions.gaussian(nest.spatial.distance, std=0.5),
"mask": {"circular": {"radius": 1.0}},
"indegree": nest.random.normal(mean=20.0, std=2.0),
"allow_multapses": True,
"allow_multapses": True,
}
cdict_dist_out = {
"rule": "fixed_outdegree",
"p": nest.spatial_distributions.gaussian(nest.spatial.distance, std=0.5),
"mask": {"circular": {"radius": 1.0}},
"outdegree": nest.spatial_distributions.gaussian(nest.spatial.distance, std=0.5),
"allow_multapses": True,
"allow_multapses": True,
}
Synapse models and properties¶
By default, Connect() creates connections using the default synapse
model in NEST, static_synapse. You can specify a different model by
adding a 'synapse_model' entry to the synapse specification
dictionary, as in this example:
nest.ResetKernel()
nest.CopyModel("static_synapse", "exc", {"weight": 2.0})
nest.CopyModel("static_synapse", "inh", {"weight": -8.0})
pos = nest.spatial.grid(shape=[10, 10])
ex_nodes = nest.Create("iaf_psc_alpha", positions=pos)
in_nodes = nest.Create("iaf_psc_alpha", positions=pos)
nest.Connect(
ex_nodes,
in_nodes,
{"rule": "pairwise_bernoulli", "p": 0.8, "mask": {"circular": {"radius": 0.5}}},
{"synapse_model": "exc"},
)
nest.Connect(
in_nodes,
ex_nodes,
{
"rule": "pairwise_bernoulli",
"p": 1.0,
"mask": {"rectangular": {"lower_left": [-0.2, -0.2], "upper_right": [0.2, 0.2]}},
},
{"synapse_model": "inh"},
)
You have to use synapse models if you want to set, e.g., the receptor type of connections or parameters for plastic synapse models. These can not be set in distance-dependent ways at present.
Connecting devices to subregions of NodeCollections¶
It is possible to connect stimulation and recording devices only to specific subregions of the layers. A simple way to achieve this is to create a layer which contains only the device placed typically in its center. When connecting the device layer to a neuron layer, an appropriate mask needs to be specified and optionally also an anchor for shifting the center of the mask. As demonstrated in the following example, stimulation devices have to be connected as the source layer.
nrn_layer = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[20, 20]))
stim = nest.Create("poisson_generator", positions=nest.spatial.grid(shape=[1, 1]))
cdict_stim = {"rule": "pairwise_bernoulli", "p": 1.0, "mask": {"circular": {"radius": 0.1}, "anchor": [0.2, 0.2]}}
nest.Connect(stim, nrn_layer, cdict_stim)
While recording devices, on the other hand, have to be connected as the target layer (see also the following section):
rec = nest.Create("spike_recorder", positions=nest.spatial.grid(shape=[1, 1]))
cdict_rec = {
"rule": "pairwise_bernoulli",
"p": 1.0,
"use_on_source": True,
"mask": {"circular": {"radius": 0.1}, "anchor": [-0.2, 0.2]},
}
nest.Connect(nrn_layer, rec, cdict_rec)
Spatially distributed NodeCollections and recording devices¶
Generally, one should not create a layer of recording devices to record from another NodeCollection with spatial extent. This is especially true for spike recorders. Instead, create a single spike recorder and connect all neurons in the spatially distributed NodeCollection to that spike recorder:
rec = nest.Create("spike_recorder")
nest.Connect(nrn_layer, rec)
Connecting a layer of neurons to a layer of recording devices as
described in the section on Connecting devices to subregions of NodeCollections, is only
possible using the pairwise_bernoulli rule. Note that voltmeter
and multimeter do not suffer from this restriction, since they are
connected as sources, not as targets.
Inspecting spatially distributed NodeCollections¶
We strongly recommend that you inspect the NodeConnections created to be sure that node placement and connectivity indeed turned out as expected. In this section, we describe some functions that NEST provide to query and visualize networks, NodeCollections, and connectivity.
Query functions¶
The following table presents some query functions provided by NEST.
|
Print the node ID ranges and model names of the nodes in the network. |
|
Retrieve connections (all or for a given source or target); see also Connectivity concepts. |
|
Returns a NodeCollection of all elements with given properties. |
|
Return the spatial locations of nodes. |
|
Obtain sources of targets in a given source layer. |
|
Obtain targets of sources in a given target layer. |
|
Obtain positions of sources of targets in a given source layer. |
|
Obtain positions of targets of sources in a given target layer. |
|
Return the node(s) closest to the location(s) in the given NodeCollection. |
|
Return NodeCollection of node closest to center of layer. |
|
Obtain vector of lateral displacement between nodes, taking periodic boundary conditions into account. |
|
Obtain vector of lateral distances between nodes, taking periodic boundary conditions into account. |
|
Write layer element positions to file. |
|
Write connectivity information to file. This function may be very useful to check that NEST created the correct connection structure. |
|
Obtain NodeCollection of elements inside a masked area of a NodeCollection. |
Visualization functions¶
NEST provides three functions to visualize networks:
Plot nodes in a spatially distributed NodeCollection. |
|
Plot all sources of a node in a given NodeCollection. |
|
Plot all targets of a node in a given NodeCollection. |
|
Add indication of mask and probability
|
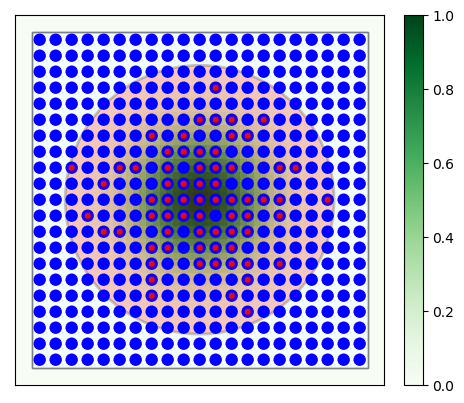
Figure 36 \(21\times 21\) grid with divergent Gaussian projections onto itself. Blue circles mark layer elements, red circles connection targets of the center neuron. The large red circle is the mask, the green distribution mark the Gaussian probability distribution.¶
The following code shows a practical example: A \(21\times21\) network which connects to itself with Gaussian connections. The resulting graphics is shown in Figure 36. All elements and the targets of the center neuron are shown, as well as mask and connection probability.
layer = nest.Create("iaf_psc_alpha", positions=nest.spatial.grid(shape=[21, 21]))
probability_param = nest.spatial_distributions.gaussian(nest.spatial.distance, std=0.15)
conndict = {"rule": "pairwise_bernoulli", "p": probability_param, "mask": {"circular": {"radius": 0.4}}}
nest.Connect(layer, layer, conndict)
fig = nest.PlotLayer(layer, nodesize=80)
ctr = nest.FindCenterElement(layer)
nest.PlotTargets(
ctr,
layer,
fig=fig,
mask=conndict["mask"],
probability_parameter=probability_param,
src_size=250,
tgt_color="red",
tgt_size=20,
mask_color="red",
probability_cmap="Greens",
)
Creating custom masks¶
In some cases, the built-in masks may not meet your needs, and you want to create a custom mask. There are two ways to do this:
To use parameters to introduce a cut-off to the connection probability.
To implement a custom mask in C++ as a module.
Using parameters is the most accessible option; the entire implementation is done on the PyNEST level. However, the price for this flexibility is reduced connection efficiency compared to masks implemented in C++. Combining parameters to give the wanted behaviour may also be difficult if the mask specifications are complex.
Implementing a custom mask in C++ gives much higher connection performance and greater freedom in implementation, but requires some knowledge of the C++ language. As the mask in this case is implemented in an extension module, which is dynamically loaded into NEST, it also requires some additional steps for installation.
Using parameters to specify connection boundaries¶
You can use parameters that represent spatial distances between nodes to create a connection
probability with mask behaviour. For this, you need to create a condition parameter that describes
the boundary of the mask. As condition parameters evaluate to either 0 or 1, it can be
used alone, with the nest.logic.conditional() parameter, or multiplied with another
parameter or value, before passing it as the connection probability.
As an example, suppose we want to create connections to 50 % of the target nodes, but only to those
within an elliptical area around each source node. Using nest.spatial.distance parameters, we
can define a parameter that creates an elliptical connection boundary.
First, we define variables controlling the shape of the ellipse.
rx = 0.5 # radius in the x-direction
ry = 0.25 # radius in the y-direction
Next, we define the connection boundary. We only want to connect to targets inside an ellipse, so the condition is
where \(x\) and \(y\) are the distances between the source and target neuron, in x- and y-directions, respectively. We use this expression to define the boundary using parameters.
x = nest.spatial.distance.x
y = nest.spatial.distance.y
lhs = x * x / rx**2 + y * y / ry**2
mask_param = nest.logic.conditional(lhs <= 1.0, 0.5, 0.0)
# Because the probability outside the ellipse is zero,
# we could also have defined the parameter as
# mask_param = 0.5*(lhs <= 1.0)
Then, we can use the parameter as connection probability when connecting populations with spatial information.
l = nest.Create('iaf_psc_alpha', positions=nest.spatial.grid(shape=[11, 11], extent=[1., 1.]))
nest.Connect(l, l, {'rule': 'pairwise_bernoulli', 'p': mask_param})
Adding masks in a module¶
If using parameters to define a connection boundary is not efficient enough, or if you need more flexibility in defining the mask, you can add a custom mask, written in C++, and add it to NEST via an extension module. For more information on writing such modules, see the NEST extension module repository.
To add a mask, a subclass of nest::Mask<D> must be defined, where D
is the dimension (2 or 3). In this case we will define a 2-dimensional
elliptic mask by creating a class called EllipticMask.
Please note that elliptical masks are already part of NEST (see
Masks). However, that elliptical mask is defined in a
different way than what we will do here though, so this can still be
used as an introductory example. First, we must include the header
files for the Mask parent class:
#include "mask.h"
#include "mask_impl.h"
The Mask class has a few methods that must be overridden:
class EllipticMask : public nest::Mask< 2 >
{
public:
EllipticMask( const DictionaryDatum& d )
: rx_( 1.0 )
, ry_( 1.0 )
{
updateValue< double >( d, "r_x", rx_ );
updateValue< double >( d, "r_y", ry_ );
}
using Mask< 2 >::inside;
// returns true if point is inside the ellipse
bool
inside( const nest::Position< 2 >& p ) const
{
return p[ 0 ] * p[ 0 ] / rx_ / rx_ + p[ 1 ] * p[ 1 ] / ry_ / ry_ <= 1.0;
}
// returns true if the whole box is inside the ellipse
bool
inside( const nest::Box< 2 >& b ) const
{
nest::Position< 2 > p = b.lower_left;
// Test if all corners are inside mask
if ( not inside( p ) )
return false; // (0,0)
p[ 0 ] = b.upper_right[ 0 ];
if ( not inside( p ) )
return false; // (0,1)
p[ 1 ] = b.upper_right[ 1 ];
if ( not inside( p ) )
return false; // (1,1)
p[ 0 ] = b.lower_left[ 0 ];
if ( not inside( p ) )
return false; // (1,0)
return true;
}
// returns bounding box of ellipse
nest::Box< 2 >
get_bbox() const
{
nest::Position< 2 > ll( -rx_, -ry_ );
nest::Position< 2 > ur( rx_, ry_ );
return nest::Box< 2 >( ll, ur );
}
nest::Mask< 2 >*
clone() const
{
return new EllipticMask( *this );
}
protected:
double rx_, ry_;
};
The overridden methods include a test if a point is inside the mask, and for efficiency reasons also a test if a box is fully inside the mask. We implement the latter by testing if all the corners are inside, since our elliptic mask is convex. We must also define a function which returns a bounding box for the mask, i.e. a box completely surrounding the mask.
The mask class must then be registered in NEST. This
is done by adding a line to the function MyModule::init() in the file
mymodule.cpp:
nest::NestModule::register_mask< EllipticMask >( "elliptic" );
After compiling and installing your module, the mask is available to be used in connections, e.g.
nest.Install('mymodule')
l = nest.Create('iaf_psc_alpha', positions=nest.spatial.grid(shape=[11, 11], extent=[1., 1.]))
nest.Connect(l, l, {'rule': 'pairwise_bernoulli',
'p': 0.5,
'mask': {'elliptic': {'r_x': 0.5, 'r_y': 0.25}}})
