Simulation behavior¶
Time-driven and event-driven approaches¶
To drive the simulation, neurons and devices (nodes) are updated in a time-driven fashion by calling a member function on each of them in a regular interval. The spacing of the grid is called the simulation resolution (default 0.1ms) and can be set using the corresponding kernel attribute:
nest.resolution = 0.1
Even though a neuron model can use smaller time steps internally, the membrane potential will only be visible to a multimeter on the outside at time points that are multiples of the simulation resolution.
In contrast to the update of nodes, an event-driven approach is used for
the synapses, meaning that they are only updated when an event is
transmitted through them (Morrison et al.
2005). To speed up the
simulation and allow the efficient use of computer clusters, NEST uses a
hybrid parallelization strategy. The
following figure shows the basic loop that is run upon a call to
Simulate():
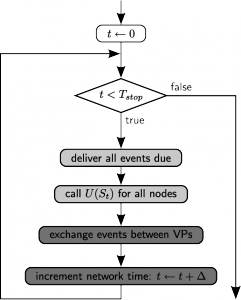
Figure 42 Simulation Loop¶
The simulation loop. Light gray boxes denote thread parallel parts, dark gray boxes denote MPI parallel parts. U(St) is the update operator that propagates the internal state of a neuron or device.
Simulation resolution and update interval¶
Each connection in NEST has its own specific delay that defines the time it takes until an event reaches the target node. We define the minimum delay dmin as the smallest transmission delay and dmax as the largest delay in the network. From this definition follows that no node can influence another node during at least a time of dmin, i.e. the elements are effectively decoupled for this interval.

Figure 43 Definitions of minimum delay (dmin) and simulation resolution (h).¶
Two major optimizations in NEST are built on this decoupling:
Every neuron is updated in steps of the simulation resolution, but always for dmin time in one go, as to keep neurons in cache as long as possible.
MPI processes only communicate in intervals of dmin as to minimize communication costs.
These optimizations mean that the sizes of spike buffers in nodes and the buffers for inter-process communication depend on dmin+dmax as histories that long back have to be kept. NEST will figure out the correct value of dmin and dmax based on the actual delays used during connection setup. Their actual values can be retrieved as kernel attributes:
nest.min_delay # A corresponding entry exists for max_delay
Set dmin and dmax manually¶
In linear simulation scripts that build a network, simulate it, carry
out some post-processing and exit, the user does not have to worry about
the delay extrema dmin and dmax as they are set automatically to the
correct values. However, NEST also allows subsequent calls
to Simulate(), which only work correctly if the content of the spike
buffers is preserved over the simulations.
As mentioned above, the size of that buffer depends on dmin+dmax and
the easiest way to assert its integrity is to not change its size after
initialization. Thus, we freeze the delay extrema after the first call
to Simulate(). To still allow adding new connections inbetween calls
to Simulate(), the required boundaries of delays can be set manually
using set():
# For co-dependent properties, we have to use `set()`
# instead of kernel attributes
nest.set(min_delay=0.5, max_delay=2.5)
These settings should be used with care, though: setting the delay extrema too wide without need leads to decreased performance due to more update calls and communication cycles (small dmin), or increased memory consumption of NEST (large dmax).
Delays after changes in resolution¶
If you change the resolution, then dmin, dmax, as well as the time-based model defaults (e.g., neuronal refractory times, synaptic delays) are adjusted to match the new resolution. In case the precision of these delays cannot be matched with the new resolution (e.g., dmin=1.6, dmax=5.3 and new_resolution=1.0), dmin is rounded down (dmin=1.0), dmax is rounded up (dmax=6.0), and the time-based model defaults are rounded mathematically. When the new resolution value is larger than a time-based model default, this value is set to the new resolution.
Note
Delays cannot be smaller than the resolution. Further, the resolution cannot be changed once model defaults have been changed or connections have been created.
Spike generation and precision¶
A neuron fires a spike when the membrane potential is above threshold at the end of an update interval (i.e., a multiple of the simulation resolution). For most models, the membrane potential is then reset to some fixed value and clamped to that value during the refractory time. This means that the last membrane potential value at the last time step before the spike can vary, while the potential right after the step will usually be the reset potential (some models may deviate from this). This also means that the membrane potential recording will never show values above the threshold. The time of the spike is always the time at the end of the interval during which the threshold was crossed.
NEST also has some models that determine the precise time of the threshold crossing during the interval. Please see the documentation on precise spike time neurons for details about neuron update in continuous time and the documentation on the connectivty concepts for how to set the delay when creating synapses.
Random numbers: Generators and seeds¶
Most NEST simulations will use random numbers, e.g., to generate Poisson spike trains or to randomize connectivity or neuronal spike emissions. NEST manages random number generators for all these purposes internally, providing separate random number streams for parallel processes automatically.
By default, NEST will use a fixed default seed to initialize all random number streams, so running the same NEST simulation script twice will give identical results. To sample the statistical variation of model dynamics, you need to set different random seeds. The following example shows this for a simple loop over different realizations:
for n in range(5):
nest.ResetKernel()
nest.rng_seed = n + 1 # seed > 0 required
# build network
# simulate network
# collect data
Valid random number seeds are numbers from \(1\) to \(2^{31}-1\).
Since random number generators, in reality, are deterministic algorithms, there is a risk that the random number streams provided by NEST contain some structure or correlations that “resonate” with a property of a neuronal network model. You should therefore always validate simulation results by simulating with different random number generators. You can see which generators are available using
nest.rng_types
To select any of the random number generator types available, use one of the following
nest.rng_type = 'mt19937'
nest.rng_seed = 12234
In the example, the generator is initialized with the default seed (or with a previously defined seed, if one was set). The second line sets the seed to a new value.
Random numbers may depend on compiler used¶
NEST uses the random number capabilities provided by the C++11 standard library. Different implementations of this library use different algorithms to generate, e.g., Poissonian- or Gaussian-distributed random numbers. Therefore, precise simulation results will depend on which implementation of the C++11 standard library you used to compile NEST. To our knowledge, three different implementations exist at present, provided respectively by GCC, Clang and Microsoft.
Split a simulation into multiple intervals¶
In some cases, it may be useful to run a simulation in shorter intervals
to extract information while the simulation is running. The simplest way
of doing this is to simply loop over Simulate() calls:
for _ in range(20):
nest.Simulate(10)
# extract and analyse data
would run a simulation in 20 rounds of 10 ms. With this solution, NEST takes
a number of preparatory and cleanup steps for each Simulate() call.
This makes the solution robust and entirely reliable, but comes with a
performance cost.
A more efficient solution doing exactly the same thing is
nest.Prepare()
for _ in range(20):
nest.Run(10)
# extract and analyse data
nest.Cleanup()
For convenience, the RunManager() context manager can handle preparation
and cleanup for you:
with nest.RunManager():
for _ in range(20):
nest.Run(10)
# extract and analyse data
Note
If you do not use
RunManager(), you must callPrepare(),Run()andCleanup()in that order.You can call
Run()any number of times inside aRunManager()context or betweenPrepare()andCleanup()calls.Calling
SetStatus()inside aRunManager()context or betweenPrepare()andCleanup()will lead to unpredictable results.After calling
Cleanup(), you need to callPrepare()again before callingRun().
Repeated simulations¶
The only reliable way to perform two simulations of a network from exactly the same starting point is to restart NEST or to call ResetKernel() and then to build the network anew. If your simulations are rather large and you are working on a computer with a job queueing system, it may be most efficient to submit individual jobs or a job array to simulate network instances in parallel; don’t forget to use different random seeds!
The following example performs simulations of a single neuron driven by a Poisson spike train using different seeds and output files for each run:
for n in range(10):
nest.ResetKernel()
nest.rng_seed = n + 1 # seed > 0 required
pg = nest.Create('poisson_generator', params={'rate': 1000000.0})
nrn= nest.Create('iaf_psc_alpha')
sr = nest.Create('spike_recorder',
params={'label': 'spikes-run{:02d}'.format(n),
'record_to': 'ascii'})
nest.Connect(pg, nrn)
nest.Connect(nrn, sr)
nest.Simulate(100)
Monitoring elapsed time¶
The progress of the simulation can be monitored by setting:
nest.print_time = True
If enabled, a line is printed to screen at every time step of the simulation to track the percentage, the absolute elapsed model time and the real-time factor, for example:
[ 25% ] Model time: 250.0 ms, Real-time factor: 2.6711
The real-time factor is defined as the quotient of wall-clock time (which
is also known as real time) and the model time (which is the duration by
which the state of the model is advanced in time, or in short, the argument to
the Simulate() call):
If the real-time factor is larger than 1 as in the example above, the simulation runs slower than the wall-clock time.
In case a simulation script contains multiple Simulate() calls,
the percentage simulation time is reset to 0% at the beginning of each call,
but the absolute model time and the real-time factor account for the total
elapsed times.
The real-time factor should not be confused with the concept of speedup. Speedup refers to a ratio of wall-clock times, namely the wall-clock time needed to solve a problem serially and the wall-clock time needed to solve the same problem in parallel (e.g., by distributing the work across multiple threads or processes):
Note
For large, distributed simulations, it is recommended to set
{"print_time": False} to avoid the overhead of the print calls.
In these cases, the real-time factor can be computed by measuring the
wall-clock time manually and dividing by the set model time.
