Warning
This version of the documentation is NOT an official release. You are looking at ‘latest’, which is in active and ongoing development. You can change versions on the bottom left of the screen.
Guide to parallel computing¶
What is parallelization?¶
Parallelization can improve the efficiency of running large-scale simulations by taking advantage of multicore/multiprocessor machines, computer clusters or supercomputers. Here we explain how parallelization is set up in NEST and how you can take advantage of it for your simulations.
NEST employs two methods for parallelization:
- Thread-parallel simulation
uses OpenMP
takes advantage of multicore and multiprocessor computers without the need for additional libraries
- Distributed simulation (or distributed computing)
uses the Message Passing Interface (MPI)
supports simulations over multiple computers
Both methods can be combined within a simulation.
See Plesser et al. (2007) for more information on NEST parallelization and be sure to check the documentation on Random numbers in NEST
Virtual processes¶
We use the concept of local and remote threads, called virtual processes. A virtual process (VP) is a thread residing in one of NEST’s MPI processes. For both thread and distributed parallelization, VPs simplify handling of neuron and synapses distributions. Virtual processes are distributed round-robin (i.e. each VP is allocated equal time slices, without any given a priority) onto the MPI processes and counted continuously over all processes.
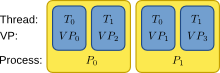
Figure 18 Basic scheme showing how threads (T) and virtual processes (VP) reside in MPI processes (P) in NEST¶
Node distributions¶
The distribution of nodes depends on the type of node.
In the figure below, a node distribution for a small network consisting of spike_generator,
four iaf_psc_alpha neurons, and a spike_recorder
in a scenario with two processes with two threads each.
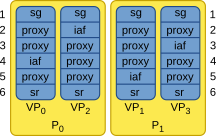
Figure 19 sg=spike_generator, iaf=iaf_psc_alpha, sr=spike_recorder. Numbers to the left and right indicate node IDs. The proxy object in the figure is a conceptual way of keeping the id of the real node free on remote processes).¶
Note
The status dictionary of each node (i.e. neuron or device) contains three entries that are related to parallel computing:
local (boolean): indicating if the node exists on the local process or not
thread (integer): id of the local thread the node is assigned to
vp (integer): id of the virtual process the node is assigned to
Neuron distribution¶
Neurons are assigned to one of the virtual processes in a round-robin fashion. On all other virtual processes, no object is created. Proxies ensure the id of the real node on a given VP is kept free.
The virtual process \(id_{vp}\) on which a neuron with node ID \(node_id_{node}\) is allocated is given by \(id_{vp} = node_id_{node} %N_{vp}\), where \(N_{vp}\) is the total number of virtual processes in the simulation.
Device Distribution¶
Devices are replicated once on each thread in order to balance the load and minimize their interaction. Devices thus do not have proxies on remote virtual processes.
For recording devices configured to record to a file (property record_to set to ascii), the distribution results in multiple data files, each containing the data from one thread. The files names are composed according to the following scheme
[model|label]-node_id-vp.[dat|gdf]
The first part is the name of the model (e.g., voltmeter or
spike_recorder) or, if set, the label of the recording device. Next is
the node ID of the recording device, followed by the id of the VP
assigned to the recorder. Spike files have the file extension gdf and
analog recordings from the multimeter have dat as file extension.
The label and file_extension of a recording device can be set like any
other parameter of a node using SetStatus().
Spike exchange and synapse update¶
Spike exchange in NEST takes different routes depending on the type of the sending and receiving node. There are two distinct cases.
Spikes between neurons¶
Spikes between neurons are always exchanged through the global spike exchange mechanism.
Neuron update and spike generation in the source neuron and spike delivery to the target neuron may be handled by different virtual processes.
But the virtual process assigned to the target_neuron always handles the corresponding spike delivery (see property
vpin the status dictionary).
Spikes between neurons and devices¶
Spike exchange to or from neurons over connections that either originate or terminate at a device (e.g.,
spike_generator -> neuronorneuron -> spike_recorder) bypasses the global spike exchange mechanism.Spikes are delivered locally within the virtual process from or to a replica of the device. In this case, both the pre- and postsynaptic nodes are handled by the virtual process to which the neuron is assigned.
Note
In an MPI-parallel simulation, the spike recorder on each MPI process only records the spikes of neurons simulated on that MPI process.
Synaptic plasticity models¶
For synapse models supporting plasticity, synapse dynamics in the
Connection object are always handled by the virtual process of the
target node.
Using multiple threads¶
Thread-parallel simulation is compiled into NEST by default and should work on all MacOS and Linux machines without additional requirements.
In order to keep results comparable and reproducible across different machines, the default mode is set to a single thread and multi-threading has to be turned on explicitly.
To use multiple threads for the simulation, the desired number of threads has to be set before any nodes or connections are created. The command for this is
nest.local_num_threads = T
Usually, a good choice for T is the number of processor cores available on your machine.
Note
In some situations, oversubscribing (i.e., to specify a local_num_threads that is higher than available cores on your machine)
can yield 20-30% improvement in simulation speed. Finding the optimal thread number for a
specific situation might require a bit of experimenting.
Multiprocessing¶
Using Python’s ``multiprocessing`` module with NEST may lead to unpredictable results!
NEST internally parallelizes network construction 1 and maintains internal data structures in this process. For
example, running several Connect() calls simultaneously can interfere with the internal parallelization and will
likely lead to unpredictable/wrong results.
Using distributed computing¶
Build requirements¶
To compile NEST for distributed computing, you will need a library implementation of MPI (e.g., OpenMPI or MPICH) on your system. If you are on a cluster or supercomputer, you most likely already have this. In case you are using a pre-packaged MPI library, please make sure that you also have the MPI development packages installed.
When using the standard installation instructions, it
is usually sufficient to add -Dwith-mpi=ON when calling cmake.
However, more detailed information on this and related flags (e.g., for
enabling the recording backend for recording to binary files) can be found in the compilation
options for distributed computing.
Please also see the generic installation instructions, where you can find an overview of all options for installing NEST.
Run distributed simulations¶
Distributed simulations cannot be run interactively, which means that the simulation has to be provided as a script. However, the script can be the same as a script for any simulation. No changes are necessary for distibuted simulation scripts: inter-process communication and node distribution is managed transparently inside of NEST.
To distribute a simulation onto 128 processes of a computer cluster, the command should look like this
mpirun -np 128 python3 simulation.py
Please refer to the MPI library documentation for details on the usage
of mpirun.
Reproducibility¶
To achieve the same simulation results even when using different parallelization strategies, the number of virtual processes has to be kept constant. A simulation with a specific number of virtual processes will always yield the same results, no matter how they are distributed over threads and processes, given that the seeds for the random number generators of the different virtual processes are the same (see Random numbers in NEST).
In order to achieve a constant number of virtual processes, NEST provides the property total_num_virtual_procs to adapt the number of local threads (property local_num_threads, explained above) to the number of available processes.
The following listing contains a complete simulation script
(simulation.py) with four neurons connected in a chain. The first
neuron receives random input from a poisson_generator and the spikes
of all four neurons are recorded to files.
import nest
from nest import Create, Connect, Simulate
nest.total_num_virtual_procs = 4
pg = Create("poisson_generator", params={"rate": 50000.0})
n = Create("iaf_psc_alpha", 4)
sr = Create("spike_recorder", params={"record_to": "ascii"})
Connect(pg, [n[0]], syn_spec={'weight': 1000.0, 'delay': 1.0})
Connect([n[0]], [n[1]], syn_spec={'weight': 1000.0, 'delay': 1.0})
Connect([n[1]], [n[2]], syn_spec={'weight': 1000.0, 'delay': 1.0})
Connect([n[2]], [n[3]], syn_spec={'weight': 1000.0, 'delay': 1.0})
Connect(n, sr)
Simulate(100.0)
The script is run three times using different numbers of MPI processes, but 4 virtual processes in every run:
mkdir 4vp_1p; cd 4vp_1p
mpirun -np 1 python3 ../simulation.py
cd ..; mkdir 4vp_2p; cd 4vp_2p
mpirun -np 2 python3 ../simulation.py
cd ..; mkdir 4vp_4p; cd 4vp_4p
mpirun -np 4 python3 ../simulation.py
cd ..
diff 4vp_1p 4vp_2p
diff 4vp_1p 4vp_4p
Each variant of the experiment produces four data files, one for each virtual process (spike_recorder-6-0.gdf, spike_recorder-6-1.gdf, spike_recorder-6-2.gdf, and spike_recorder-6-3.gdf). Using diff on the three data directories shows that they all contain the same spikes, which means that the simulation results are indeed the same independently of the details of parallelization.
References¶
- 1
Ippen T, Eppler JM, Plesser HE and Diesmann M (2017). Constructing neuronal network models in massively parallel environments. Front. Neuroinform. 11:30. DOI: 10.3389/fninf.2017.00030